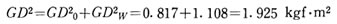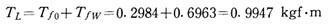制御における
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
制動距離(回転角度)
いま,制御軸が n0rpm で回転し、直線運動部分が v0 m/minで移動している装置の状態を考え、制御軸に設けたブレーキを作動させて、制御軸を n rpm 速度をv m/min に減速する間の制動に必要な総回転角度と移動距離を求める。
制動時間中に制御軸が何回転するかを考えてみる。
制動に要する制御軸の総回転数は、軸回転速度と時間の関係から求められる。
制動に必要な制御軸の総回転数を表わす式を導くものとすると、時間は一般に秒単位で求められるので、回転速度も秒単位すなわち毎秒回転数rpsで表わし、GD2、トルクなどもすべて制御軸 i に関する等価GD2,、トルクとして、表わすと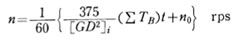
初速 n0 rpmで回転する制御軸に、ΣTBの制動トルクを作用させた場合、t秒間に軸が nB 回転したとすると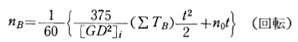 
展開して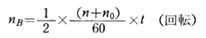
制動開始後 t秒間に制御軸が回転する回転 nBは、初期回転速度 N0 rps と
t 秒後の回転速度 N rpsの平均値に、所要時間 t を掛けたものに等しい。 制動所要時間を与える式を上式に代入し、時間 t を消去して nB を表わすと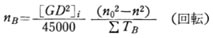 
加速制御
加速制御の場合は一般に機械装置の動力源としてモータが用いられ、起動トルクが必ずしも一定ではないため、多少やっかいになる。
出力トルクー定の動力源を用いる場合は別にして、モータを動力源とする場合は、各種モータの選定、トルクー回転数(速度)特性について負荷トルクの特性と合わせて、モータ関係の専門技術者と詳細に検討することが望ましい。
まず加速トルクが一定とした場合の基本的な考え方について述べ、ついで加 速トルクが軸回転数,時間で変化する場合について述べる。
加速(起動)時間
加速の所要時間を求める場合の条件は、 加速トルク、等価負荷トルク、等価抵抗トルク、装置の等価GD2および回転数(速度)条件である。
加速トルクが一定である場合を考える。
時間とトルク、 GD2の関係は制動、加速の区別にかかわらず
基本式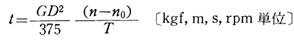
で 表わされる。
[TM]i : 制御軸に関するモータの等価加速トルク(kgf・m)
[TL]I : 制御軸に関する等価負荷トルク(kgf・m)
[Tf]I : 制御軸に関する等価抵抗トルク(kgf・m)
[TA]I : 制御軸に関する正味加速トルク(kgf・m)
[GD2]I : 制御軸に関する装置の等価GD2(kgf・m^2)
とすれば 加速に作用する正味加速トルクは、モータトルクから制動に作用する各トルクを差引いて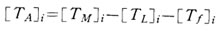
n0 : 初期軸回転数(rpm)
n : 加速後の回転数(rpm)
t : 加速時間(Sec)
とすれば 式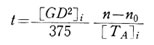
において、一般に各トルクはすべて正の値(絶対値)を用いてよい。
ただし,等価負荷トルクが傾斜コンベアなどで、加速トルクに作用するような場合では、[TL]iを負の値として上式で計算する必要がある。
なお、起動時間を求める場合は、当然ながら n0 = 0 とすればよい。
加速制御で制御軸のモータトルクが時間的に軸回転数の変化に伴って変化する場合について考える。
最も簡単でよく用いられる手法は、平均加速トルクを求めて、加速時間を計算する方法である。
この平均加速トルクを求めるには、概算的に加速開始時のモータトルクと最大モータトルクを平均するものと、モータのトルク - 回転数曲線と負荷 - 回転数曲線より図式的に求める方法とがある。
TM0 : 加速開始時のモータトルク(kgf・m)
TM max : 加速時間中の最大モータトルク(kgf・m)
TL max : 加速時間中の最大負荷トルク(含抵抗トルク)(kgf・m)
TL min : 加速時間中の最少負荷トルク(含抵抗トルク)(kgf・m)
として、それぞれ平均モータトルク TM mean 、平均負荷トルク TL meam を求めれば
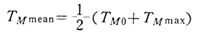
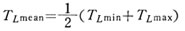
これらの平均値として、平均加速トルク TAmeanを次式で求めれる。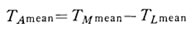
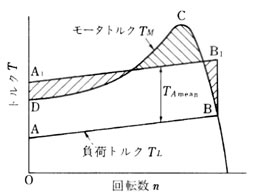右図に示すようなモータトルク TM と負荷トルク TL (抵抗トルクTfを含む)の トルク - 回転数特性が、与えられているものとする。
nr は、モータトルクと負荷トルクが等しくなった安定回転速度(rpm)である。
エネルギの観点から考えてすぐわかるように 加速に使用されるエネルギは、TM とTLで囲 まれた部分ABCDである。
このエネルギが装置の運動エネルギに変換されることになる。
したがって加速エネルギを示す面積を、負荷トルク TL に添ってならした直線A1 B1 (負荷トルクが曲線ならば曲線)を図の上で求め、右および左上がりの斜線部の面積を等しくなるようにすると、ABとA1 B1の差が平均加速トルクT Ameanとなる。
この方法は、かなり正確になる。
以上のようにして求めた平均加速トルクを用いれば、加速時間 t は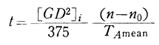
モータの起動トルクの特性曲線は、モータメ一カに依頼すれば、一般に入手できるが、 単に電流計で電流を計測してある程度推定できる。 電磁電流が一定の場合、モータの起動トルクは電流に比例するので、
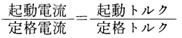と考えれば、電流値の変化より起動トルク - 回転数(時間)の特性曲線を推定することが可能である。
例) テーブル装置の加速時間
テーブル装置において、重量Wの加工物を載せて起動する場合、所定の速度 v となるまでの所要時間を求める。
以下のデータでGD2,トルク,回転数などはすべて制御軸に関して換算した等価の数値とする。
加工物重量 : W= 700kgf
送り速度 : v = 90m/min
装置のGD2 : GD2_0 = 0.817kgf・m^2
抵抗トルク : Tf0 = 0.2984 kgf・m
平均モータトルク : TM mean = 3.75kgf・m
ガイド部摩擦係数:μ = 0.05
軸の安定回転数 : n = 720rpm
加工物の重量Wによる等価GD2、GD2_w と等価抵抗トルクの増加量 Tfw を求めると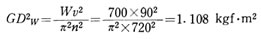
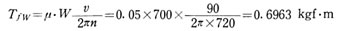
したがって、加工物を乗せたテーブル装置の等価GD2、等価負荷(抵抗)トルクTLは 
＜＜ 