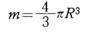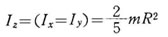慣性モーメント
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
慣性モーメントは、私にとっては難問です。 この中には、実際の設計には、まず使用しないだろうと思われる計算式の成り立ちから説明してあります。
都度の導きたいケースにあった公式を引っ張り出してきてパラメーターを入れていくことでも、ほとんどの場合、対応できると思いますが材料力学の時も同じなのですが、どこのパラメーターを変更することにより一番 効率的に要求される条件に近づけられるかと言う場合には、やはり、理論的な部分を理解することが必要となります。
物体の回転運動において慣性モーメントは非常に重要なもので、設計においては、この慣性モーメントと同一の性質をもつものをGD2(ジー・ディスクエア)と呼んで実際の計算を行っている。
慣性モーメント I (Kgf.s^2 m) との関係は
GD^2(Kgf.m^2) = 4 g I で表される
慣性モーメントの計算法
対称形の物体の慣性モーメント 形状にはさまざまなものが考えられるが、特別なものを除いて一般にいくつかの基本的な形状、円柱や直方体たどを組合わせて構成されていると仮定し計算する。
1 ) 円柱(円板)
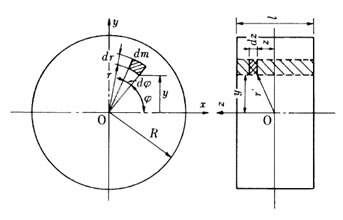 右図に示すような円柱を考え、 回転軸を2軸として慣性モーメントを求めることにする。
右図に示すような円柱を考え、 回転軸を2軸として慣性モーメントを求めることにする。
以下のように 記号を用いると
R : 円柱の直径
γ: 回転軸から任意の徴少部分までの距離
I : 円柱の長さ
ψ : 微少部分の位置角
p: 密度
dm : 徴少部分の質量
m : 円柱の全質量
dI : z軸に関する微少部分の慣性モーメント
Iz : z軸に関する円柱の慣性モーメント
γ,ψの徴少分をdγ,dψとして、z軸から距離rにある体積 I・dr・rdψの微笑部分をとれば,
質量dmは、 dm = pIrdrdψ
この徴少部分の慣性モーメントは dI = r2dm = pIr3drdψ したがって円柱全体では、 ここに、円柱の全質量は次式で与えられるので m = pπR2I
z軸に関する円柱の慣性モーメントは Iz = 1/2・mR2
以上のように物体の微少部分を考え、その部分の回転軸に関する小さな慣性モーメン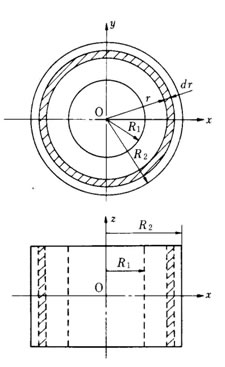 トを求め、ついで全体にわたってこれを集めれば、すなわち連続体の場合積分すれば、全体の慣性モーメントが求まることになる。
トを求め、ついで全体にわたってこれを集めれば、すなわち連続体の場合積分すれば、全体の慣性モーメントが求まることになる。
2) 中空円柱
右図に示すような中空円柱の場合、以下のように記号を定めると
R1 : 中空円柱の内半径
R2 : 中空円柱の外半径
微少部分として図示のような薄肉円筒を考えれば、この部分の微少質量は、 dm = 2πplrdr
したがって中空円柱の慣性モーメント この中空円柱z軸に関する慣性モーメント Izは、 円柱の場合と同様にしてx,y軸に関する慣性モーメント Ix, Iy は
3) 直方体
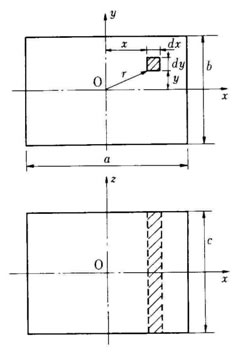 機械装置における回転体は・一般に円柱(板)形状のものが多いが,形鋼や角材など直方体を組合せた形状のものもある。
機械装置における回転体は・一般に円柱(板)形状のものが多いが,形鋼や角材など直方体を組合せた形状のものもある。
これらの形状の物体の慣性モーメントを求める場合、その基礎となるのが直方体の慣性モーメントである。
右図において、直方体の中心軸を x ,y, z 軸とし、それぞれの長さを a, b, c とする。 この場合、回転軸として x, y, z 軸のいずれを選んでも相対的に同じことになるが、いま z軸を回転軸として、慣性モーメント Iz を求 めてみよう。
右図における徴少部分の質量 dmは、物体の密度を ρとして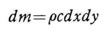 この徴少部分と回転軸(Z軸)との距離γは、
この徴少部分と回転軸(Z軸)との距離γは、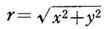 であるから
であるから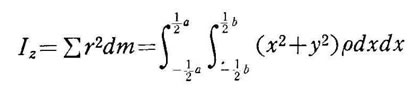
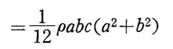 一方、直方体の全質量 m は
一方、直方体の全質量 m は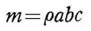 したがって、z軸に関する慣性モーメソトは
したがって、z軸に関する慣性モーメソトは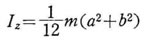 x, y 軸に関する慣性モーメントIx, Iy は、 Iz と同様な方法によって求めることができるが,もっと簡単に軸の間の相関性を利用して、軸を x→ z 、 z → y 、 y → x に変換し、a → c 、 c → b、 b → c と置きかえれば,軸xに関する慣性モーメント Ixは
x, y 軸に関する慣性モーメントIx, Iy は、 Iz と同様な方法によって求めることができるが,もっと簡単に軸の間の相関性を利用して、軸を x→ z 、 z → y 、 y → x に変換し、a → c 、 c → b、 b → c と置きかえれば,軸xに関する慣性モーメント Ixは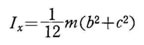 同様にして
同様にして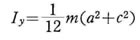
4) 楕円柱
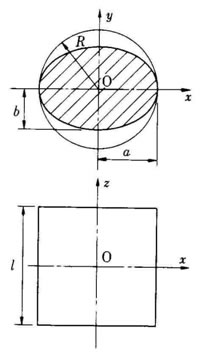 機械装置の部品には、アームなど楕円形状の断面をもつものがある。
機械装置の部品には、アームなど楕円形状の断面をもつものがある。
楕円柱形状の物体の償性モーメントは、円柱の慣性モーメントを求めたように、任意の微少部分をとり積分を行って得ることができるが、円柱形状物体の慣性モーメントから容易に類推できる。
右図に示すような楕円柱を考え、重心を通る軸、x, y, z 軸 を定める。
円柱の場合との相違に着目すると、半径Rがπ軸 について長半径になり、y軸については短半径になっている。
これらの関係により、x軸、y軸 に関する慣性モーメント Ix, Iy は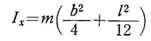
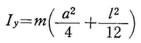
z軸に関しては 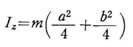 と考えれば良いので
と考えれば良いので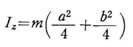
5) 球
球の場合は、その中心を通る軸はすべて対称中心線となるので 右図において、x, y, z 軸に関する慣性モーメン トは同一となる。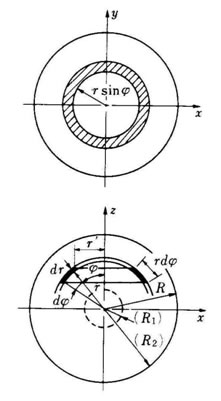
いま、2軸に関する慣性モーメソトを求めてみよう。
球 の半径をRとし、任意の位置(τ,ψ)に微少なリング状の 部分を考えれぱ、この部分の質量 dm と z軸からの距離 γ' は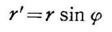 、
であるから、この徴少部分の
、
であるから、この徴少部分の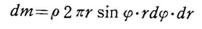 z軸に関する小さな慣性モー メント dI は
z軸に関する小さな慣性モー メント dI は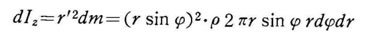
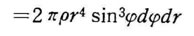
したがって球全体ではτ,ψを0~R、0~πの間で積分すれば 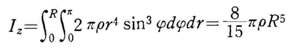 球全体の質量 m は、次式で与えられるので
球全体の質量 m は、次式で与えられるので