ベクトルについて
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
大きさと向きを考える量をベクトルと言う。
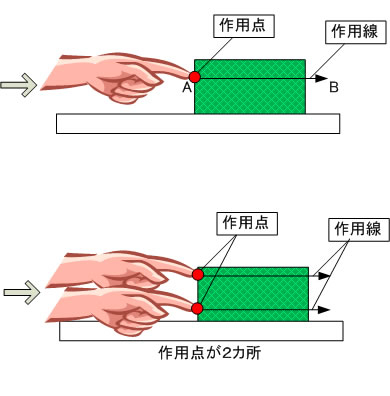
(力だけに限らない) ある物体を指で押そうとした場合 指と物体のあたる箇所を 作用点 押そうとする方向を 作用線と呼ぶ。
指2本で押した場合 作用点は2カ所になる。
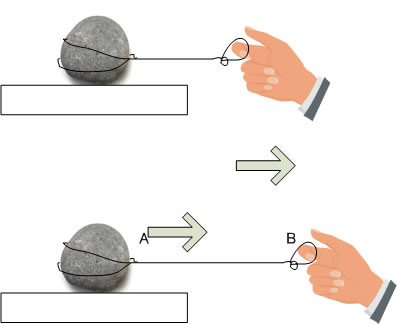
石に紐をくくりつけて 引っ張る場合も同じで上と同じように石は右に動きます。
引っ張る方向が作用線になり力が同じであれば 糸の長さを変えても同じように動きます。糸の長さに影響はされません。
このように、ベクトルは、大きさを線分の長さで示し、向きを矢印のついた線分(有向線分)で表します。
点Aと点Bを両端とする有向線分の向きがAからBに向かう向きのとき、この有向線分の表すベクトルをとする。
このとき、ベクトルの出発点になっているAを始点、ベクトルの行き先になっているBを終点と言う。
力の分解について
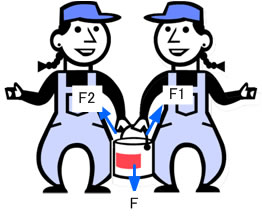
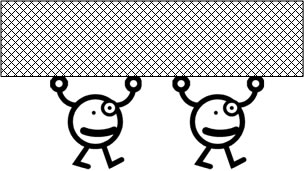一人で持てない重たい物を二人だと持てるようになります。 これは物体の重さが二つに分けられるからです。
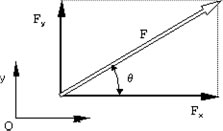1つの力Fを、それと同じ働きをする2つの力F1、F2 に分けることを力の分解という。
力F1、F2を力Fの分力または成分という。 直角な2つの力へ分解して考えるこもよくあります。
力の合成について
2つの力F1、F2 が1点に働いている場合、この2つの力による効果と同じ働きをする1つの力Fを、F1、F2の合力という。F1、F2 からFを求めることを、力の合成という。
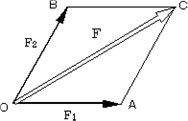右図 に示すようにF1、F2をとなり合う2辺とする平行四辺形を描く。
この平行四辺形を「力の平行四辺形」とよび、その対角線が求める合力である。
このようにベクトルは力の方向、大きさを効率よく表してくれる。
矢印の長さは決められておらず 基準となる長さに(力に対して相対関係になる。) 100kgfの力であれば100mmとして書いておくと 結果の長さが 150mmであれば 150Kgとなる。
力の合成、分解を考える上で非常に有用な ツールとなるので是非 使い方をマスターしましょう。
ベクトル演習１
ベクトルは、作図して求めるのが一番 確実、簡単です。
しかし、時として正確な数値を求められるときもあります。
計算値を作図した値で確認するのが一番、間違いのない方法です
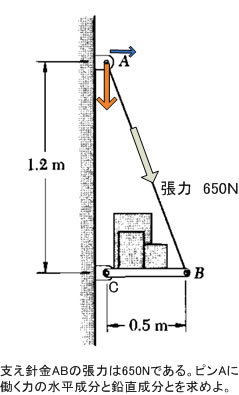
右の設問 は、実際の設計でもよくある例です。
３角関数は、必須ですね。 まず∠BACの角度を出しましょう。
いつでも役に立つ公式 θ=tan-1(y/x)－＞tan-1(0.5/1.2) = 22.6° あとは 計算してみてください。
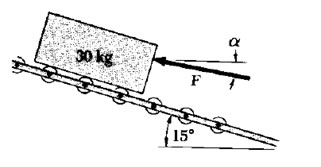図示の梱包(つりあっている)を支える最小の力Fの大きさと方向とを決定せよ。
ただし，ローラから梱包 に作用する力は，斜面に垂直であるとする。 梱包を自由物体に選ひ，とれを質点とみなLて取扱ってもよいと仮定する。
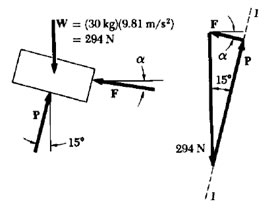この場合の自由物体図を描く。
つりあいの条件 自由物体には，3力だけが働くから、これらつりあっているととを示す力の3角形を描く。
線分1-1はFの既知の方向を表す。
力Fの最小値を求めるため、 P方向に垂直にFの方向を選ぶ。