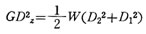各種形状のGD2
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
慣性モーメントの計算法については、質量のような力学的な量を用いるより、物体の重量を用いたほうが、何かと取扱いが便利であり実際的である。
したがって、質量を用いて表わされる慣性 モーメントではなく、工学 (重力)単位で表わすのを、GD2(ジーディスクエア)と呼んでいる。
GD2は、慣性モーメントと同じく、物体の回しにくさ、あるいは回転している物体の止 めにくさを表わすので、GD2をフライホイール効果とも言われる。
慣性モーメントとGD2の関係
慣性モーメントとGD2の換算
GD2に おけるDは、回転半径に対する回転直径のようなものであって、 k が回転体の半径そのも のではないように、Dも回転体の直径そのものを表わしているのではない。
慣性モーメント I は、物体の質量 m と回転半径 k によって表わすことができるが、いま回転体の重量をGとし、重力の加速度を g とすれば、質量 mは、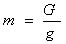
いま、D を回転半径に k に対して
回転直径とすると、
D = 2k したがって、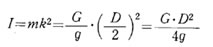
となり
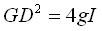で与えられる。
GD2の単位は重力単位で表わした場合
GD2=4 x g [m /s2] x I [kgw・s2m] = 4gI [Kgw.m2] (kgf・m2)
すなわち、GD2は重力単位では(kgw・m2)または(kgf・m2)の単位で表わされる。
実際には計算のたびに回転半径を求めてGD2を計算するのは、大変面倒であるので GD2を ある量を表わす一つの記号として扱い、各種形状に応じて慣性モーメントを求め、 GD2に換算することがよく行われる。
GD2における平行軸の定理
物体の重量をWとし、物体の重心を通る軸に関するGD2をGD2 0 とすると、慣 性モーメントにおける平行軸の定理を表わす
式と、上述の換算式から、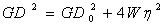
上式は、実際の設計において複雑な形状の物体を簡単な形状の物体の組合せに置き換え特定の回転軸に関するGD2を計算する場合に非常に便利な公式である。
さまざまな形状の物体のGD2
円柱(円板)形状の物体のGD2
回転軸が物体の重心を通る場合 いま直径D(m)、長 さL(m),重量W(kgf)の円柱柱を考える。
回転軸が円柱の軸中心線 z に一致した場 合のGD2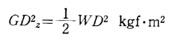
を求めることにする。
この場合、慣性モーメント Iz は 換算すると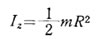 
で表される。
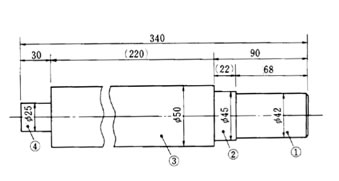右に示す形状寸法の段付軸がある。 こ の軸の軸中心線に関する GD2を,具体的に数値を 用いて計算してみる。
材質は炭素鋼S30C,比 重(量)τ=7.86(gf/cm3) とする。 形状より・1~4の4つの円柱体に分割して、計算すればよい。 添字1,2,・・・...は、そ れぞれ部分1,2・・・...に関するものとする。
1 :
2 :
3 :
4 :
合計 
回転軸が物体の重心を通らない場合
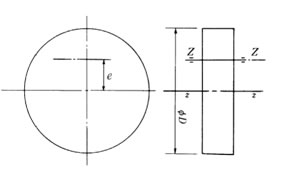円板カムや偏心軸の設計においては、円板や軸の中心線に回転軸が一致しない。
右図に示すような円板カムのGD2を求めてみよう。
重量をW(kgf)とする。 重心を通るz軸に関するGD2z は、
GD2 = 1/2 WD^2
回転軸Z と z軸間の距離(偏心量)を e(m)とすれば、
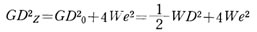展開して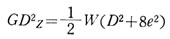
上式は、円柱形状物体において、回転軸がその物体の中心軸に平行で、eだけ離れている場合の GD2を求める公式である。
なお、この回転軸は必ずしも物体の内部にある必要はなく、物体の外部に離れて存在しても同様である。
以下に述べる様々な形状物体の場合でも同じである。
円柱体の中心軸に垂直で、重心位置からηだけ離れた回転軸をもつ場合について考る。
プーリのアームの回転に相当する場合である。
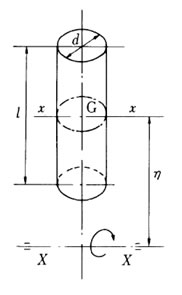右図に示すように、直径d(m)、長さL(m)、重量W(kgf)の 円柱が図示のようにηだけ離れたX軸のまわりに回転するものとする。 まず、重心を通るκ軸に関するGD2、は
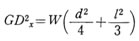したがって、X軸に関するGD2xは、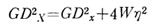
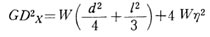となります。
中空円柱(板)形状の物体のGD2
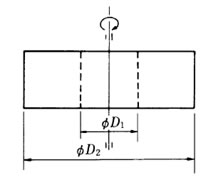回転軸が物体の重心を通る場合
右図に示すような重量W(kgf)、内径 D1(m)、外径 D2(m) の回転体を考え、このGD2を求める。
慣性モ一メント I 1は、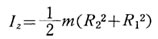
したがって、 GD2は、
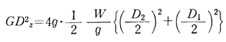展開して