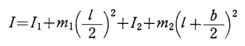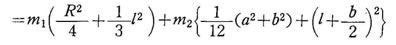平行軸の定理
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
一般の公式集に示された慣性モーメントは、基本的な円柱、角柱形状の物体について、 その重心を通る座標軸に関して示されたものである。
機械装置において物体が回転する場合、必ずしも物体の中心を通る軸のまわりに回転するとは限らず、中心軸からある距離だけ離れた位置に、回転軸が設けられていることも多い。
また,実際の設計では、複雑な形状の物体について慣性モーメントを計算しなければならないことも多いが、その場合は基本的な形状の物体を組み合わせたものとして計算するのが普通である。
ここでは、平行軸の定理すなわち任意の軸に関する慣性モーメントの求め方について、説明します。
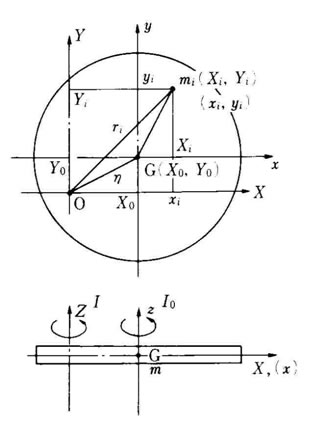
いま右図に示すように物体の中心(重心)Gを通る軸を z軸とし、O点を通りこれと平行な任意の回転軸を z軸 として、それぞれ x, y軸を定める。
原点0よりみて,ri だけ離れた位置(Xi, Yi }つにある徴少質量物の z軸 に関する慣性モーメント ΔI は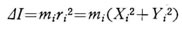
したがって、物体全体のZ軸に関する慣性モーメント I は 
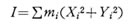この物体の重心Gの座標を(X0, Y0)とし、徴少質量物の位置を mi の位置をx, y 座標系で(xi, yi)とすれば、図より分るように、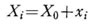
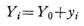であるから、慣性モーメントは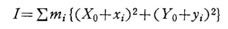
右図を参照すれば分るように、全体で左右の一次モーメントが釣合う位置が重心軸(y軸)といえる。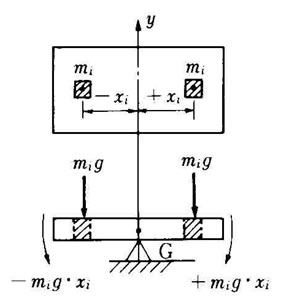
同様に考えれぼ、x軸に関しても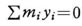
となる。 これら重心軸 x, y軸の交点Gが重心(重心点)である。
すなわち、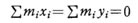
また、重心Gを通る z軸に関する慣性モーメント Ioは、
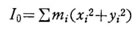となるから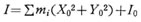 
ここに、Σmi はこの物体の全質量 m であり、ηを原点0から重心Gまでの距離とすれば、次式の関係が成立するので
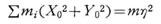となり、結局この物体の2軸に関する慣性モーメソト I は,、式で与えられる。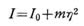
すなわち、任意の平行軸に関する慣性モーメントは、重心を通る軸に関する慣性モーメ ントに、全質量 m とこれら両軸間の距離の2乗η2の積を、加えれぱ求められることにな る。
こ
の関係を平行軸の定理といい、 応用上非常に重要である。
ここで,、この定理の利用法を示す簡単な例を示す。
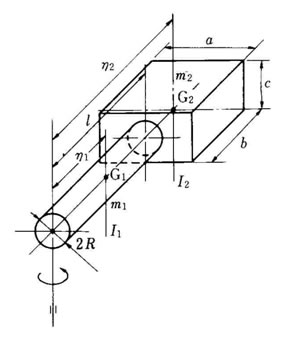
例〕:組み合わせ形状物体の慣性モーメント 右図に示すような質量m1 の円柱と質量 m2 の直方体を組み合わせた物体の慣性モーメントを求めてみる。 それぞれの物体の重心G1,G2を通り、回転軸に平行な軸に関する慣性モーメントI1,12は、
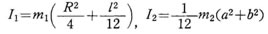また、それぞれの物体の重心までの距離は η1=L/2 , η2 = L+ b/2であるから、全体の慣性モーメント I は 
