運動
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
運動の第一法則 (慣性の法則)
「外部から力が働かないか、あるいはいくつかの力が働いていてもそれらの力がつり合っていれば、静止している物体はいつまでも静止をつづけ、運動している物体はいつまでも等速直線運動をつづける」
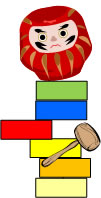
右の”だるま落とし”は この法則を良く表しています。
赤の駒を一瞬に はじき飛ばすと上と下の駒は、その場にとどまり真ん中の駒だけがとばされます。
他の駒が その場に静止し続けようとしていることが証明されます。
運動の法則(運動の第二法則)
「物体に力が働くとき、物体には力と同じ向きの加速度が生じる。
その加速度αの大きさは、働いている力の大きさFに比例し、物体の質量mに反比例する」
加速度 α = 外力 F / 質量 m
外力 F = 質量 m X 加速度 α
物体が重たいと加速しにくく 軽いと加速しやすいと言うことですね。
この加速度は 増えるばかりでなくマイナスも含みます。
重たい物は 止まりにくいと言うことです。
運動の第三法則 (作用反作用の法則)
「大きさが等しく方向が反対に働く力を作用反作用といい、作用が働くところには必ず反作用がある」
運動の定義
運動とは物体がある時間を経過した時に位置を変えることを運動と言います。
物体が動く経路により運動の種類が分かれます。
1, 直線運動 (落下運動も含む)
2, 曲線運動
3,回転運動
4,放物線運動 (ボールを投げたときに描くカーブの運動)
物体が動く速度により運動の種類が分かれます。
1,等速度運動
2,加速度運動
速度と加速度/角速度と円運動
速度(はやさ )= 距離/時間 V = s / t | ω = θ/ t
距離 = 速度 X 時間 s = V x t | θ = ω x t
時間 = 距離/速度 t = s / V | t = θ / ω
加速度 = (後の速度 - 最初の速度) / 時間の経過
α = ( V2 - V1 ) / t α
θ = ( ω2 - ω1 ) / t
角速度 (単位時間に回るに角度) = 回った角度 / 要した時間
角速度は ω(オメガ)を用い単位記号に〔rad/s〕を用いる。
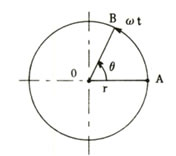
右図において腕rがOを中心としてA点からt秒後に角AOB, 即ち, θ〔rad〕回転してB点に達したとすると, 角速度ω(オメガ)は ω= θ / t (rad/s) となる。
したがって, ω〔rad/s〕の角速度でt〔s〕秒間回転すれば弧度θ〔rad〕は θ=ωt となる。 1 rad = 360 / ( 2. π) = 57.3° です。
角度をなぜ ラジアンで表記するかと言えば 孤の長さ= 半径 x rad で 表せるからです。
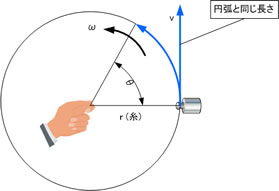
半径を1 とすると 全円の孤は 2π です。 (あたりまえなのですが) 周速度 接線方向に移動する速度 右の図では半径 r の糸の先におもりをつけて角速度 ωで回転している時糸が切れた場合おもりは接線方向へ飛びます。そのときの速度が周速度です。
角速度が一定ならば糸の長さ(半径)が長いほど早くなります。
QDY1) 速度60Km/hの自動車の速度が3秒後に30Km/hになった場合の加速度は、幾つでしょうか?
QDY2) 速度72Km/hで走行中の自動車に急ブレーキをかけて40m走って止めた。 このときの加速度と停止に要した時間を求めてください。
