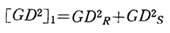車軸換算の等価GD2
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
輸送車両や台車,移動クレーンなどのように、装置そのものが移動する場合、速度制御や停止制御などブレーキ装置を直接車軸に取り付けて行う例は、非常に多い。
この場合、当然ながら制御を行う車軸に関する等価GD2が必要になる。
このGD2を一般に車軸換算のGD2と呼んでいる。
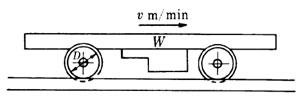右図に示すような台車を考え、つぎのように記号を定める。
W : 車輪の重量をも含めた台車全体の重量(kgf)
v : 台車の走行速度(m/min)
n : 車軸の回転数(rpm)
D : 車輪の直径(m)
[GD2]
w : 車軸換算のGD2(kgf・m^2)
車輪の回転数 n と走行速度の関係は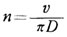
直線運動体の等価GD2を求める式により
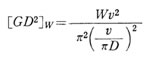展開して
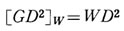
上式からわかるように、車軸換算のGD2は直線運動の速さや車軸の回転数に関係なく、台車の全重量Wと車輪径Dによって簡単に求まる。
一般に車軸換算のGD2には駆動装置や車輪などの回転運動に関するGD2は考慮してない。 しかしながら、実際の設計では車輪に連動するすべての運動体のGD2を考えておかなけれぽならないので、車輪とこれに連動する駆動系の車軸に関する等価GD2を求め、これと台車のGD2を合わせて車軸換算のGD2ということもある。
各種の設計資料などではこの車軸換算のGD2ではなく、等価慣性モーメソト Iw として表わされている場合も多い。
この場合は、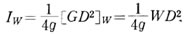
例) 台車の車軸換算GD2
自重 8.5 ton(車輪の重量も含む)車輪径 600mm の台車がある。
稼動時は台車上に 2.6 ~ 6.3 tonの荷を積載するものとする。
この場合の車軸換算GD2を計算する。 重量 : 台車自重と積荷重量を合わせて、直線運動を行う重量とする。
W=8500+(2600~6300)=11100~14800kgf
車軸換算[GD2]w : [GD2]w = WD2 = (11100 ~ 14800) x 0.62 = 3996 ~ 5328 kgf・m^2
回転体と直線運動体が連動する装置の等価 GD2
一般の機械装置においては、直線運動を行う部分をもつ場合でも回転運動によって駆動され、回転運動が何らかのメカニズムによって直線運動に変換されたものと考えることができる。
これらの装置の慣性問題を取り扱う場合は、当然ながら直線運動部分の慣性と回転運動部分の慣性をあわせて考えねばならない。
ここに
m : 装置を構成する回転軸の数
m' : 装置を構成する直線運動体の個数
n i : 特定の制御軸 i の回転数(rpm)
n j : 任意の回転軸 j の回転数(rpm)
v j : 任意の直線運動体の移動速さ(m/min)
GD2 j : 任意の回転軸
jに属する回転体のGD2(kgf・m^2)
W j' : 任意の直線運動体の重量(kgf)
j , j' : 任意の整数1,2,・・・...,m (m')
具体的な例をとって、実際の設計でこうした問題を扱う際の考え方を示しておく。
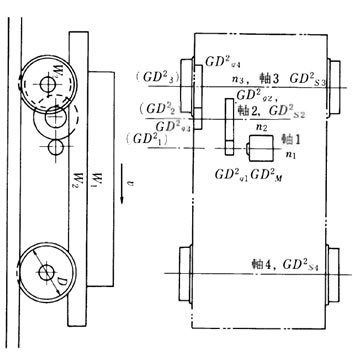
例1〕台車装置全体のモータ軸換算の等価GD2 右図に示す台車装置全体の駆動モータ軸に関する等価GD2を求める。 駆動系における歯車や軸、モータなどのそれぞれの軸に関するGD2は、すでに計算されているものとする。
v (m/min) : 台車走行速度(モータ軸1の回転数 n,rpmのとき)
W 0(kgf) : 台車の総自重(車輪4個、駆動装置系全体の重量を含む)
W 1(kgf) : 積荷の重量
W 2(kgf) : 車輪1個の重量
D (m) : 車輪の直径
GD2_M(kgf・m^2) : モータのGD2(モータ軸1のGD2を含む)
GD2_q1~GD2_q4(kgf・m^2) : 歯車G1~G4のGD2
GD2_s2 ~ GD2_s4(kgf・m^2) : 軸2~4のGD2
n1 ~ n3 (rpm) : 軸1~3の回転数
このような場合は、回転運動部と直線運動部に分けて考え、さらに各軸ごとのGD2にまとめ、最終的に換算したい特定軸(例題ではモータ軸)に関する等価GD2を求める。
回転運動部分:
軸1に関するGD2 : 軸1に属する回転体は、モータと歯車G1であるから、そのGD2を GD2_1とすれば、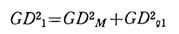
軸2に関するGD2 :
軸2に属する回転体は、軸2、歯車G2、歯車G3であるから、その GD2_2は,
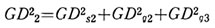
軸3に関するGD2 :
軸3に属する回転体は、軸3、車輪2個、歯車G4である。 GD2_3 は、車輪1個のGD2_wを求めて、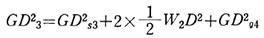
軸4に関するGD2 :
直接駆動軸に連結されてない軸4と2個の車輪のGD2は、一見慣性と無関係に考えられるが、エネルギーの観点から考えればすぐわかるように、装置全体のたかに含まれるものである。
そのGD2の大きさは、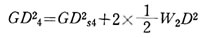
以上の回転運動体のGD2を、軸1(モータ軸)に関する等価GD2にすべて換算し、その合計をGD2_Rとすれば、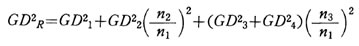
直線運動部分:
直線運動を行う部分の軸1に関する等価GD2_sは、重量が台車の総自重 W0と積荷の重量 W1であり、その速さ v は、毎分当り移動距離で与えられているので、直線運動体の等価GD2を求める。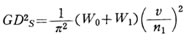
台車装置全体の等価GD2:
以上に求めた、回転運動部と直線運動部のモータ軸1に関する等価GD2を合計すれば、 装置全体の等価[GD2]1となる。