図心と重心
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
物体は多くの質点の集まりであり各質点はその質量に 比例する重力の作用線を受ける。
この平行線の合体を物体の重量といい この着力点を重心という。
(重心の定義) 任意の1点に紐をつけて垂らし紐の延長線上に線を引き 次の別の場所を同じように垂らし 別の 延長線を引きます。 2本の交点がその形状の重心となります。
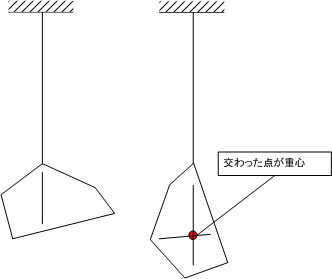 均一の物体では 重心 = 図心 となりますが均一でない物体は図心と重心は一致しない。
均一の物体では 重心 = 図心 となりますが均一でない物体は図心と重心は一致しない。
これは つり下げた糸を中心に 左右均等な受領配分になっているこを示しています。
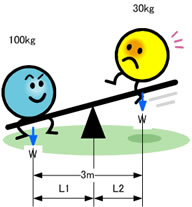 左右均等な重心バランスを考える場合 右のようなシーソーで考えてみましょう。
左右均等な重心バランスを考える場合 右のようなシーソーで考えてみましょう。
左の重量を100kg 右を30kg 2者間の距離を 3mとします。
バランスする支点の距離は不明です。
これを 式に すると 100 X L1 = 30 X L2 です。
L1 + L2 = 3 なので L1 = 3 - L2 となり 先の式に代入し 100 X ( 3- L2) = 30 X L2 300 - 100. L2 = 30 L2 -> 300 = 130.L2 , L2 = 2.3m となります。
 これと考え方は同じで面積を考慮した物が下記になります。
これと考え方は同じで面積を考慮した物が下記になります。
X, Y方向をそれぞれ 求めて 図心を出します。
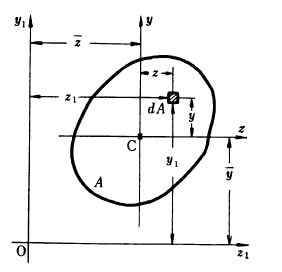
面積 A の図形を考え図心 C を通る直行軸を y, z これに平行な任意の直行軸を y1, z1 とし図形内の微小面積を dA とすれば重心の定義によって
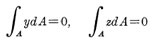 ここで y1 , z1 軸から図心までの距離を
ここで y1 , z1 軸から図心までの距離を 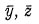 とすれば
とすれば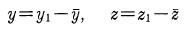 であるからこれを 上記式に代入し
であるからこれを 上記式に代入し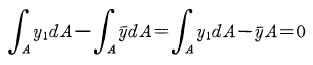 ここから
ここから となります。
今は、CADが進んでおりこのような計算を する事は ほとんどありませんが 重心とは、図心とは何なのかを 理解することは重要です。
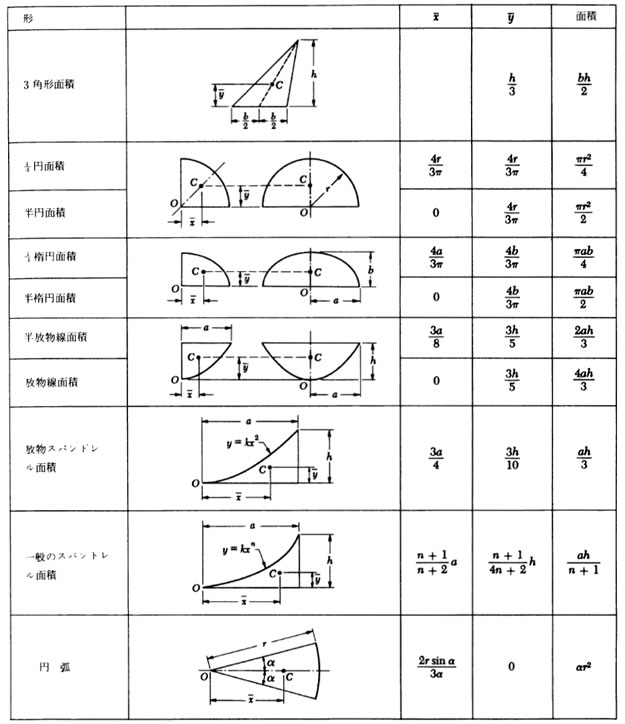
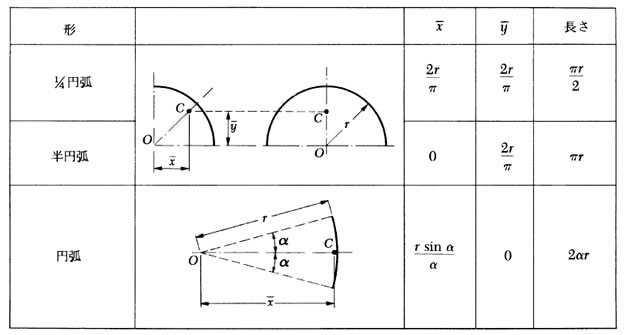
参考に図心の公式を下記に示します。
となります。
今は、CADが進んでおりこのような計算を する事は ほとんどありませんが 重心とは、図心とは何なのかを 理解することは重要です。
参考に図心の公式を下記に示します。