測定における誤差と対策
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
例えば加工中の軸径をマイクロメータで測定するのは、その外径の真の値を知りたいためである。
しかし現実には種々の原因によって,測定値は真の値を示さない。
この両者の差が誤差である。 すなわち 測定値 - 真の値 = 誤差 である。 誤差はその原因によって、次のように分類できる。
1,被測定物による誤差
2, 過失による誤差
3,系統誤差
4, 偶然誤差
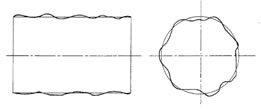
1、の被測定物による誤差 は例えば軸の外径ならば右図に示すような真円度・円筒度などの幾何学的な形状誤差によるものであって 測定箇所を限定して測定した場合に問題となり、この場合は測定箇所と測定回数を増やすことによって解決できる。
2,過失による誤差 は読み取り、記録などの際の測定者の過失あるいは事故によるものであって測定の際に十分注意を払うことによって解決できる。
結果的に誤差の本質として残るのは、3,の系統誤差と 4、の偶然誤差の二つである。
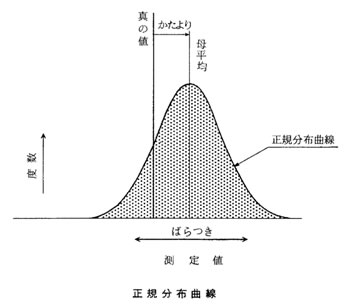一般に系統誤差と偶然誤差とが原因となって生ずる総合的な誤差の分布は 右図に示す正規分布曲線によって表されることが知られている。
図の横軸は各測定値を表し、縦軸は多数回の測定を行って横軸に示す各測定値が何回現れたか、すなわち度数を表す。
図から、正規分布曲線は山型の中央がもっとも高く(これを母平均と呼ぶ)、そこから離れるにつれて低くなり、さらに左右対称の形をしていることがわかる。
この正規分布曲線の左右の広がりをばらつきと言い、母平均の真の値からのずれを かたよりと言う。
測定値にかたよりが生ずる原因は、系統誤差による。 系統誤差は、測定器の定期的な精度検査や校正を行うこと、また測定者の教育 訓練などを行うことによってある程度は取り除くことができる。
このようにして系統誤差を取り除いたとしてもなお残るものが、やはり偶然誤差であり これによって測定値はばらつきを生ずる。
偶然誤差は言葉の意味する通り 明確につきとめることのできない多数の偶然に基づくものと考えられるが これをなくすことはできない。
そこで偶然誤差に対しては,正規分布曲線の左右対称性に注目し 何回かの測定をくり返してそれらの算術平均を求めれば真の値が推定できることになる。
しかし 一般には上述の系統誤差によるかたよりが修正しきれないで残っているために 単純に算術平均値をもって真の値と呼ぶことには注意を要する。
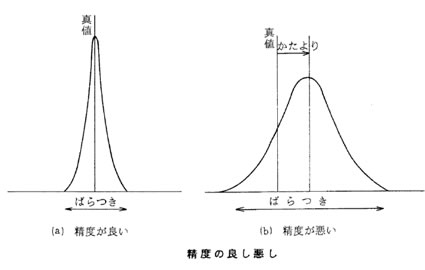
そこでJIS (日本工業規格)では ばらつき(偶然誤差)が小さく、 かつ かたより(系統誤差)が小さいものほど "精度が良い" と定義している。
下図の例で言えば (a) の方が (b) よりも ばらつきも かたよりも 小さいので、(a)の方が (b)よりも精度が良いと言う。
