幾何公差
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
「幾何公差」の重要性と理解が困難な理由
１、NC技術の向上により部品加工もより複雑で高精度のものを求められるようになってきている。
２、寸法公差のみの指示では、正確な形状、形体を指示できない。
３、データムの基本を理解するうえで、実際の測定方法の知識が不足している。
寸法公差測定に比べて幾何公差測定方法は、測定物の設置方法、把持方法など多岐にわたる
４、世の中に幾何公差の曖昧な図面、間違った図面があふれている 。
実はこの4番目の理由が一番 幾何公差の浸透を妨げていると思われます。
本解説の最後に具体例を示しますが、幾何公差の解説書には定義、解釈が細かく書かれていますが、実務で使用される図面例と、かけ離れていて、図面例になりえない。逆に、実務に近い
製図図書参考にある幾何公差は間違いだらけであり、これも参考とはならないのが現状です。
しかし、今後、幾何公差の重要性はますます、大きくなることでしょう。
このような状況なので、たとえ正確な幾何公差の指示ができている図面を作成したとしても加工者も正確な理解をして加工できるとは、考えにくいことでしょう。
設計者から加工者への説明がしばらくの間、必要と思われます。
「幾何公差」って何？
実際の部品は図（a）のように断面が真円に仕上がらないことが多い。
図（b）のような軸心の方でも， もしこれが曲がっていたならば， いかに各部が
寸法公 差の範囲内に仕上がっていても、 組み立てるこ とができない場合も生じてくる。
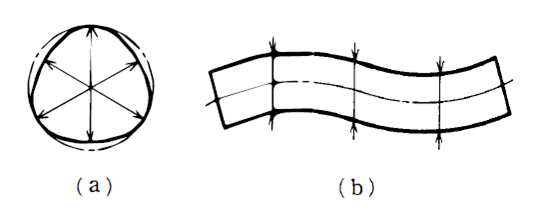
このような穴と軸の場合に限らず、一般に品物は、面とか線とかの幾何学的な形体を有しているが、これらの形体を幾何学的に正確に仕上げることは不可能であるから、どの程度までの狂いならば許容できるかについて定めておき、これを図面に指示しておく必要がある。
このような、形体の狂いに対する許容値を、 幾何公差という。
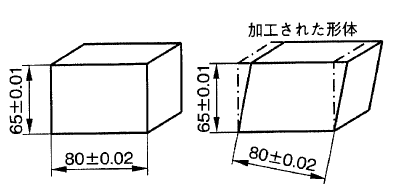直方体に寸法公差 が指示されたとき、その寸法公差を守って直方体が加工されたとしても、歪んで加工されて適正に組み立てられない場合がある。
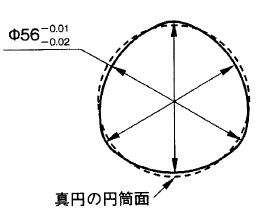円筒表面の加工法によっては、 その横断面が図 に示すおにぎり形の等径ひずみ円に加工されることがある。
円筒軸の表面が等径ひずみ円に 加工されたとき、 その円筒軸の様々な方向の直径をマイクロメータで測定する と、 円形形体のひずみが検出されないために、図示された寸法公差を充分に満たす測定結果が得られたにもかかわらず、 相手の穴部品に挿入されずに組立てが不可能になることがある
事例に示したように、 機械部品の寸法公差を指示しても、 部品の加工誤差を管理できるとは限らない。
設計者の意図を機械部品に正しく反映させるには、 必要に応じて適切な幾何公差を設計図面に指示が必要となる。
幾何公差は， 単独形体と関連形体とがあり、 前者は他の部分と無関係に公差を指定することができる。
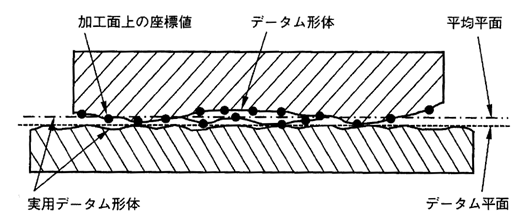
後者では、 関連する相手があって、 それとの関係で公差が適用されるので、 この公差を指示するために、 仮に設定した理論的 に正確な幾何学的基準をデータムという。
実際にはそのような正確なデータムは存在しないから、 実用上ではたとえば相手側の面とか定盤とかをもって代用し、 これらをデータム形体とか実用データム形体と呼んでいる。
幾何公差の図示の基本
付加記号：幾何公差の指示に付加して用いる記号
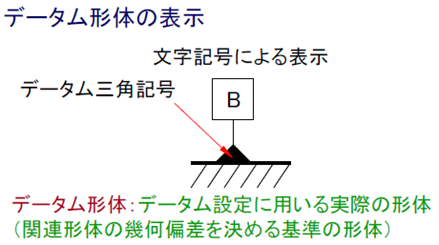
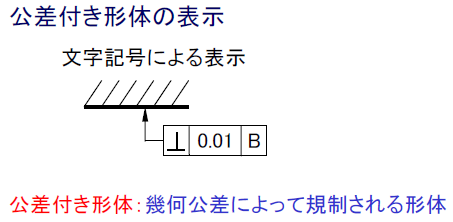
公差記入枠による表示
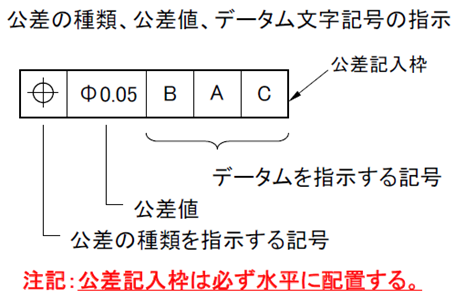
| 適用する形体 | 幾何公差の種類 | 記号 | 定義 | |
| 単独形体 | 形状公差 | 1.真直度公差 |  |
直線形体の幾何学的に正しい直線からのひらきの許容値。 |
| 2.平面度公差 |  |
平面形体の幾何学的に正しい平面からのひらきの許容値。 | ||
| 3.真円度公差 |  |
円形形体の幾何学的に正しい円からのひらきの許容値。 | ||
| 4.円筒度公差 |  |
円筒形体の幾何学的に正しい円筒からのひらきの許容値。 | ||
| 単独形体 | 5.線の輪郭度公差 |  |
理論的に正確な寸法によって定められた幾何学的輪郭からの線の輪郭のひらきの許容値。 | |
| 関連形体 | 6.面の輪郭度公差 |  |
理論的に正確な寸法によって定められた幾何学的輪郭からの面の輪郭のひらきの許容値。 | |
| 関連形体 | 姿勢公差 | 7.平行度公差 |  |
データム(注)直線またはデータム平面に対して平行な幾何学的直線または幾何学的平面からの平行であるべき直線形体または平面形体のひらきの許容値。 |
| 8.直角度公差 |  |
データム直線またはデータム平面に対して直角な幾何学的直線または幾何学的平面からの直角であるべき直線形体または平面形体のひらきの許容値。 | ||
| 9.傾斜度公差 |  |
データム直線またはデータム平面に対して理論的に正確な角度をもつ幾何学的直線または幾何学的平面からの理論的に正確な角度をもつべき直線形体または平面形体のひらきの許容値。 | ||
| 位置公差 | 10.位置度公差 |  |
データムまたは他の形体に関連して定められた理論的に正確な位置からの点、直線形体、または平面形体のひらきの許容値。 | |
| 11.同軸度公差 |  |
同軸度公差は、データム軸直線と同一直線上にあるべき軸線のデータム軸直線からのひらきの許容値。また、同心度公差は、データム円の中心に対する他の円形形体の中心の位置のひらきの許容値。データム軸直線またはデータム中心平面に関して互いに対称であるべき形体の対称位置からのひらきの許容値。 | ||
| または同心度公差 | ||||
| 12.対称度公差 |  |
|||
| 振れ公差 | 13.円周振れ公差 |  |
データム軸直線を軸とする回転体をデータム軸直線のまわりに回転したとき、その表面が指定された位置または任意の位置において指定された方向に変位する許容値。 | |
| 14.全振れ公差 |  |
データム軸直線を軸とする回転体をデータム軸直線のまわりに回転したとき、その表面が指定された方向に変位する許容値。 | ||
| (注)データム:形体の姿勢公差、位置公差、振れなどを決めるために設定した理論的に正確な幾何学的基準(関連形体の場合に必要) | ||||
各幾何公差の図示例、解釈を示します。
- 真直、平面、真円度
- 円筒、線、面の輪郭度
- 平行度
- 直角、傾斜度
- 位置度
- 同軸、対象度
- 円周触れ度
1.真直度公差(線の真直度公差) |
|
| 公差域の定義 | 図示例とその解釈 |
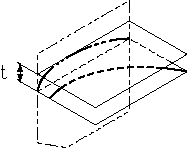
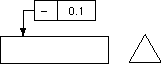
| 公差域は、一つの平面に投影されたときには、tだけ離れた2つの平行な直線の間に挟まれた領域である。 | 指示線の矢で示した直線は、矢の方向に0.1ミリだけ離れた2つの平行な平面の間になければならない。 |
 |
 |
 2.平面度公差 |
|
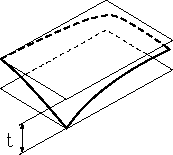
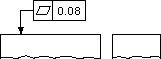
| 公差域の定義 | 図示例とその解釈 |
| 公差域は、tだけ離れた2つの平行な平面の間に挟まれた領域である。 | この表面は、0.08ミリだけ離れた2つの平行な平面の間になければならない。 |
 |
 |
 3.真円度公差 |
|
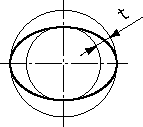
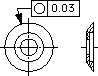
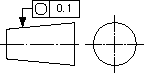
| 公差域の定義 | 図示例とその解釈 |
| 対象としている平面内での公差域は、tだけ離れた2つの同心円の間の領域である。 | 外径面の任意の軸直角断面における外周は、同一平面上で、0.03ミリだけ離れた2つの同心円の間になければならない。 |
 |
 |
| 任意の軸直角断面における外周は、同一平面上で0.1ミリだけ離れた2つの同心円の間になければならない。 | |
 |
|
 4.円筒度公差 |
|
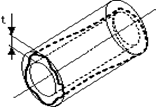
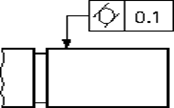
| 公差域の定義 | 図示例とその解釈 |
公差域は、tだけ離れた2つの円軸円筒面の間の領域である。
|
対象としている面は、0.1ミリだけ離れた2つの円軸円筒面の間になければならない。 |
 |
 |
 5.線の輪郭度公差(単独形体の線の輪郭度公差) |
|
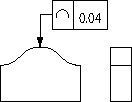
| 公差域の定義 | 図示例とその解釈 |
| 公差域は、理論的に正しい輪郭線上に中心をおく、直径tの円がつくる2つの包路線の間に挟まれた領域である。 | 投影面に平行な任意の断面で、対象としている輪郭は、理論的に正しい輪郭をもつ線の上に中心をおく直径0.04ミリの円がつくる2つの包路線の間になければならない。 |
 |
 |
 6.面の輪郭度公差(単独形体の面の輪郭度公差) |
|
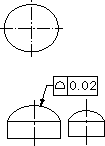
| 公差域の定義 | 図示例とその解釈 |
| 公差域は、理論的に正しい輪郭面上に中心をおく、直径tの球がつくる2つの包路面の間に挟まれた領域である。 | 対象としている面は、理論的に正しい輪郭をもつ面の上に中心をおく、直径0.02ミリの球がつくる2つの包路面の間になければならない。 |
 |
 |
 7.平行度公差(データム直線に対する線の平行度公差) |
|
| 公差域の定義 | 図示例とその解釈 |
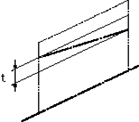
公差域は、1つの平面に投影されたときには、データム直線に平行でtだけ離れた2つの平行な直線の間に挟まれた領域である。
|
指示線の矢で示す軸線は、データム軸直線Aに平行で、かつ、指示線の矢の方向(垂直な方向)にある0.1ミリだけ離れた2つの平面の間になければならない。 |
 |
 |
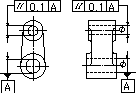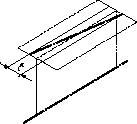
| 指示線の矢で示す軸線は、データム軸直線Aに平行で、かつ、指示線の矢の方向(水平な方向)にある0.1ミリだけ離れた2つの平面の間になければならない。 | |
 |
 |
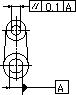| 公差の指定が互いに直角な2つの平面で行われている場合には、この公差域は、断面t1×t2で、データム直線に平行な直方体の中の領域である。 | 指示線の矢で示す軸線は、それぞれの指示線の矢の方向、すなわち、水平方向に0.2ミリ、垂直方向に0.1ミリの幅をもち、データム軸直線Aに平行な直方体内になければならない。 |
 |
 |
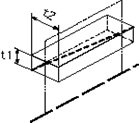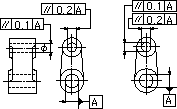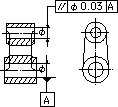
| 公差を示す数値の前に記号φが付いている場合には、この公差域は、データム直線に平行な直径tの円筒の中の領域である。 | 指示線の矢で示す軸線は、データム軸直線Aに平行な直径0.03ミリの円筒形になければならない。 |
 |
 |
 8.直角度公差(データム直線に対する線の直角度公差) |
|
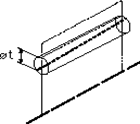| 公差域の定義 | 図示例とその解釈 |
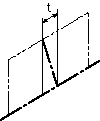
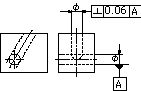
| 公差域は、一平面に投影されたときには、データム直線に垂直で、tだけ離れた2つの平行な直線で挟まれた領域である。 | 指示線の矢で示す傾斜した穴の軸線は、データム軸直線Aに垂直で、かつ、指示線の矢の方向に0.06ミリだけ離れた2つの平行な平面の間になければならない。 |
 |
 |
 9.傾斜度公差(データム直線に対する線の傾斜度公差) |
|
| 公差域の定義 | 図示例とその解釈 |
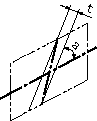
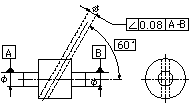
| (a) 同一平面内の線とデータム直線 一平面に投影されたときの公差域は、データム直線に対して指定された角度で傾き、tだけ離れた2つの平行な直線の間に挟まれた領域である。 | 指示線の矢で示した穴の軸線は、データム軸直線A-Bに対して理論的に正確に60°傾斜し、指示線の矢の方向に0.08ミリだけ離れた2つの平行な平面の間になければならない。 |
 |
 |
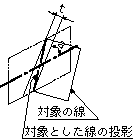
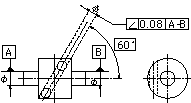
| (b) 同一平面内にない線とデータム直線対象としている線とデータム直線とが、同一平面上にない場合には、この公差域は、データム直線を含み、対象としている線に平行な平面へ、対象としている線を投影したとき、データム直線に対して指定された角度で傾き、tだけ離れた2つの平行な直線の間に挟まれた領域である。 | データム軸直線A-Bを含み、指示線の矢で示した穴の軸線に平行な平面への穴の軸線の投影は、データム軸直線A-Bに対して理論的に正確に60°傾斜し、指示線の矢の方向に0.08ミリだけ離れた2つの平行な直線の間になければならない。 |
 |
 |
 10.位置度公差(点の位置度公差) |
|
| 公差域の定義 | 図示例とその解釈 |
公差域は、対象としている点の理論的に正確な位置(以下、真位置という)を中心とする直径tの円の中または球の中の領域である。
|
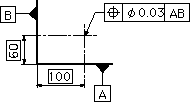
指示線の矢で示した点は、データム直線Aから60ミリ、データム直線Bから100ミリ離れた真位置を中心とする直径0.03ミリの円の中になければならない。なお、この図例の場合は、データム直線A、Bの優先順位はない。 |
|
 |
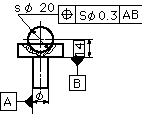
| 備考) 図に現れている面に垂直方向の厚みを考慮に入れるときは、ここに説明した円は円筒となり、点は線となる。指示線に矢で示した球の中心は、データム軸直線Aの線上でデータム平面Bから14ミリ離れた真位置に中心をもつ、直径0.3ミリの球の中になければならない。 | |
 |
|
 11.同軸度公差または同心度公差 |
|
| 11.1同軸度公差 | |
| 公差域の定義 | 図示例とその解釈 |
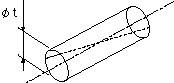
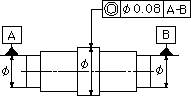
公差を示す数値の前に記号φがついている場合には、この公差域は、データム軸直線と一致した軸線をもつ直径tの円筒の中の領域である。
|
指示線の矢で示した軸線は、データム軸直線A-Bを軸線とする直径0.08ミリの円筒の中になければならない。 |
 |
 |
| 11.2同心度公差 | |
| 公差域の定義 | 図示例とその解釈 |
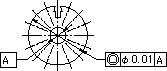
公差域は、データム点と一致する点を中心とした直径tの円の中の領域である。。
|
指示線の矢で示した円の中心は、データム点Aを中心とする直径0.01ミリの円の中になければならない。 |
 |
 |
 12.対称度公差(データム中心平面に対する面の対称度公差) |
|
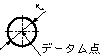| 公差域の定義 | 図示例とその解釈 |
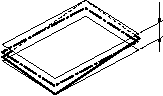
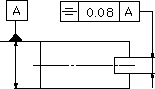
公差域はデータム中心平面に対して対称に配置され、互いにtだけ離れた2つの平行な平面の間に挟まれた領域である。
|
指示線の矢で示した中心面は、データム中心平面Aに対称に0.08ミリの間隔をもつ、平行な2つの平面の間になければならない。 |
 |
 |
 13.円周振れ公差(半径方向の円周振れ公差) |
|
| 公差域の定義 | 図示例とその解釈 |
|
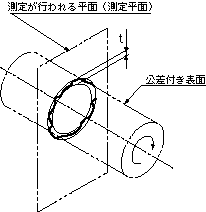
公差域は、データム軸直線に垂直な任意の測定平面上でデータム軸直線と一致する中心をもち、半径方向にtだけ離れた2つの同心円の間の領域である。振れは一般には、軸線の周りの完全な一回転について適用されるが、一回転のうちの一部分に適用を限定することもできる。 |
指示線の矢で示す円筒面の半径方向の振れは、データム軸直線A-Bに関して一回転させたときに、データム軸直線に垂直な任意の測定平面上で、0.1ミリを超えてはならない。 |
 |
 |
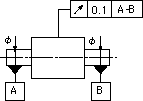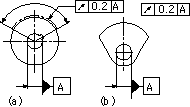
| 指示線の矢で示す円筒面の一部分[図(a)では太い一点鎖線で示す範囲、図(b)では扇形の円筒部分]の半径方向の振れは、公差付き形体部分を、データム軸直線Aに関して回転させたときに、データム軸直線に垂直な任意の測定平面上で0.2ミリを超えてはならない。 | |
 |
|
 14.全振れ公差(半径方向の全振れ公差) |
|
| 公差域の定義 | 図示例とその解釈 |
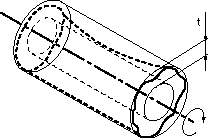
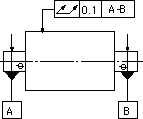
| 公差域は、データム軸直線に一致する軸線をもち、半径方向にtだけ離れた2つの同軸円筒の間の領域である。 | 指示線の矢で示す円筒面の半径方向の全振れは、この円筒部分と測定具との間で軸線方向に相対移動させながら、データム軸直線A-Bに関して円筒部分を回転させたときに、円筒表面上の任意の点で0.1ミリを超えてはならない。測定具または対象物の相対移動は、理論的に正確な輪郭線に沿い、データム軸直線に対して正しい位置で行われなければならない。 |
 |
 |
幾何公差の付加記号
幾何公差の相互関係
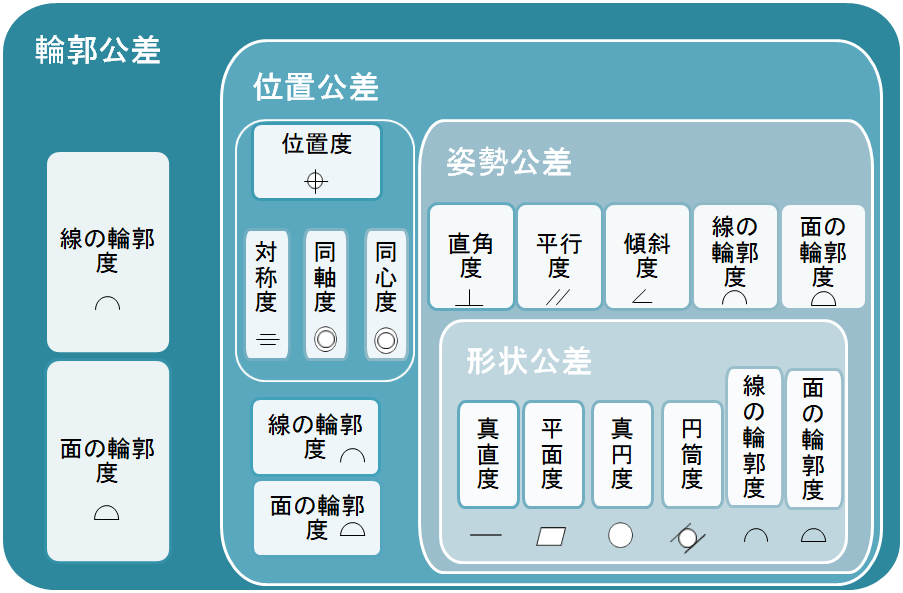
データム不要の形状公差が一番下位に位置し、次に形状公差を含む姿勢公差が上位に位置し、次に形状公差および姿勢公差を含む位置公差がその上位に位置する。
最上位にすべて包含する輪郭公差が位置する。つまり、輪郭公差は代替特性として、形状公差、姿勢公差および位置公差のいずれにも適用可能である。
ただし、輪郭公差は、形体が点、軸線、中心面などの誘導形体には適用できない。
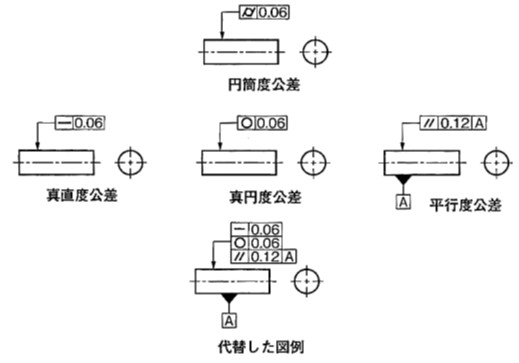
円筒度公差は円筒表面の形状の狂いを規制するので、真直度、真円度のすべてを規制することと同じである。
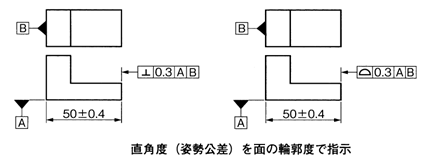
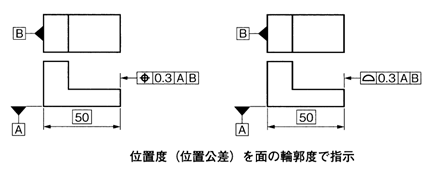
形状公差 < 姿勢公差 < 位置公差 でなければならない理由は、この関係が維持されなければ規制に矛盾が生じてくるためである。 例を下記に示す。
＞＞
＞＞