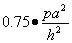引張と圧縮(その他の応力)
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
 引っ張りと圧縮
引っ張りと圧縮
引張り応力
右のシャンデリアをつっているクサリには、シャンデリアの重みがかかっていますから、この重みに対して切れまいとする応力が生じています。
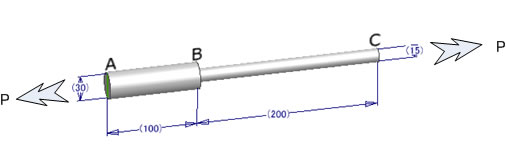
下図のようなアルミ段付き棒に 引張り荷重 P=600kgが作用するとき全長はいくつになるでしょうか?
このような場合は AB間、BC間と断面形状が違うかたまりずつで考えます。
AB間の断面の面積は 30^2 X π / 4 = 706.85mm2 BC間は 15^2 X π /4 = 176.71mm2
アルミの 縦弾性係数 E = 0.72 X 10^4kg/mm2 とします。
AB間は 長さ 100mm なので P.L / A.E = (600 X 100) / ( 706.85 X 0.72 X 10^4) = 0.0113mm
BC間は 長さ 200mm なので P.L / A.E = (600 X 200) / ( 176.71 X 0.72 X 10^4) = 0.0943mm
合計 0.0113 + 0.0943 = 0.1056mm の 伸びとなリます。
 自重を受ける物体
自重を受ける物体
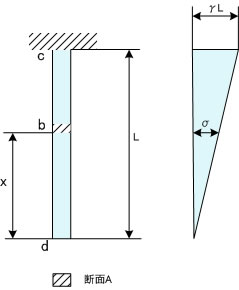
右図のように一様な断面を持った物体(棒)が上からつり下げられていた場合物体の重さは単位体積あたりの重さをγとすれば W = γ.Lである。
この場合外力が加わっていなくとも物体は引張りを受ける。
先端dからxの距離にある断面bにはdb間の重さ σ = γxがかかる。
重さ(応力)は長さに沿って一次的に変化し 固定端 cで最大になる。
σ MAXがこの棒の引張り強さに達すれば棒は破断する。
この棒の引張り強さが40kg/mm2 γ=7.86 X 10^-6kg/mm3 とすれば L = σ/ γ なので
40/ 7.86 X 10^-6 = 5.1 X10^6 mm = 5100m となります。
通常の状態の形状では自重は無視してよいほどの応力になります。
引っ張り強度計算例(ネジの強度)
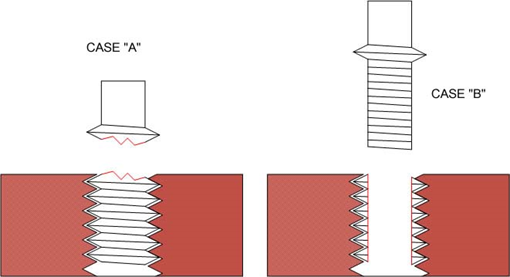 ネジの破壊は右のように二通り発生します。 おねじが破断する場合とネジ山が坊主になる場合です。
ネジの破壊は右のように二通り発生します。 おねじが破断する場合とネジ山が坊主になる場合です。
これは多くの場合十分なめねじ長さが無かったときや、下穴が適正でなかった場合、または材質がもろかった場合などに多く起きます。
左のケースのCASE "A"の強度計算はネジの谷径の断面積でかかる力を割ります。
M10のネジの谷の断面積は8.376^2Xπ/4=55.1mmなので最大許容荷重はこの断面積に材料の降伏点荷重をかけて安全率で割ることとなります。 ネジの安全率は通常 静荷重 3 、 衝撃荷重 12です 。
従いM10のネジでSS400のネジであれば降伏点は24Kg/mm2ですから 55.1 X 24 / 3 = 441Kg(静荷重) 55.1 X 24 / 12 = 110Kg(衝撃荷重) がM10の許容荷重となります。 並目ねじ寸法表
CASE "B"の場合はやや複雑になります。
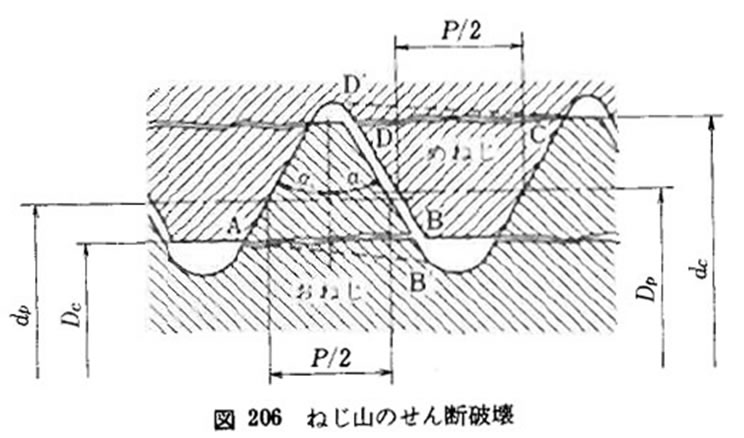
下の図に沿って一山あたりの剪断長さを求めます。
AB = (P/2) + (dp - Dc ) tan α / CD = (P/2) + (dc - Dp) tan α とし、 オネジのネジ山が剪断破壊する荷重をWB 、メネジのネジ山が剪断破壊する荷重をWNとすると WB = πDc . AB . zτb / WN = πdc . CD . zτn で示される。
ここで z は負荷能力があると見なされる山の数、τb, τnはメネジ、オネジそれぞれの断破壊応力となります。
M10 の有効長さ 10mmとした場合、山数は ピッチ 1.5mmなので 10/1.5で6.6 山
AB = (P/2) + (dp - Dc ) tan α = (1.5/2)+(9.026-8.376) X tan 30 = 1.1253
SS400の引張り強さ 400N/mm2ですから上の表より0.5倍とし20.4Kgf/mm2とします。
WB = πDc . AB . zτb = π X 8.376 X 1.1253 X 6.66 X 20.4 = 4023Kgf でネジ山が破断します。
安全係数をかけて 4023 / 3 = 1341Kg(静荷重) 4023 / 12 = 335Kg(衝撃荷重)
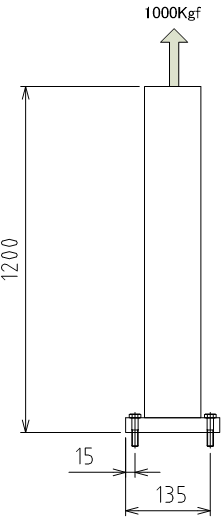
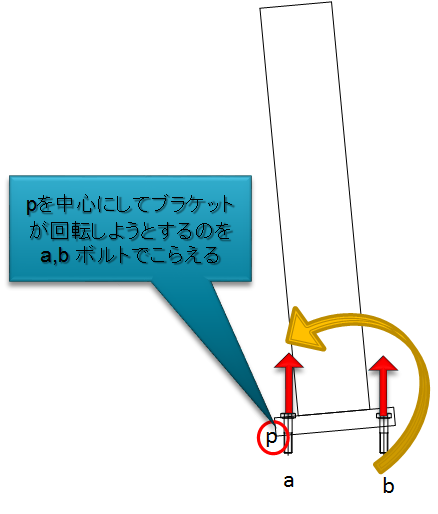
次に右のようなケースを考えてみます。
上方向へ1000kgfで引っ張りが生じた場合 4本のボルトで支える場合
単純に1000 / 4 = 250kgf/1本 となります。
ところが外力が横からかかるとすると
p点でのモーメント 1200 x 1000 = 1200000kgf.mm このモーメントをp-a & p-b の距離で割る ボルト4本とすると 1200000 / (2 x (15 + 135)) = 4000Kg /1本 の引っ張り力が各ボルトに生じます。
圧縮応力
パイスで何かを締めつけるとき材料とバイスにはそれぞれ同じ大きさの応力が生じます。
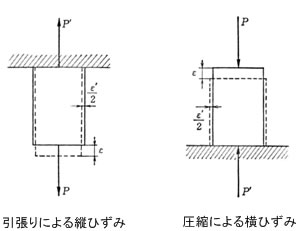
 ほとんどの材質では引張り強さと圧縮強さは同等です。
ほとんどの材質では引張り強さと圧縮強さは同等です。
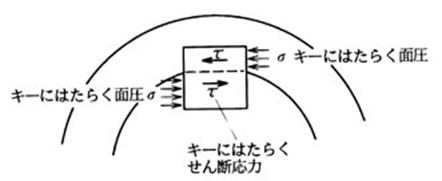 圧縮強度計算例(キーの面圧と剪断)
圧縮強度計算例(キーの面圧と剪断)
1KN・mのトルクがφ50の軸にかかった場合の面圧計算例 (キー長さは50mmとする)
φ50には16X10のキーが適用されます キーにかかる力は 1KN X 1000 / 25 =40KN
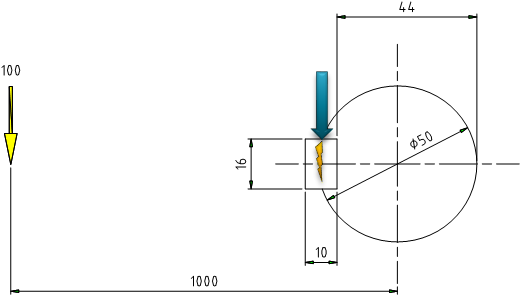 キーの受圧面積は10/2X50=250mm2
キーの受圧面積は10/2X50=250mm2
40KNを250mm2の面で受けるため 40KN / 250 = 160N/mm2
この式を整理すると (4.T)/( t. L . d )
T = トルク、 t = キー高さ (全高)、 d = 軸の直径、 L = キー長さ
(4 X 1KNX1000) / (10 X 50 X 50) = 160N/mm2 (面圧)
剪断方向の面積は16 x 50 =800mm2 40KNを800mm2で剪断力を受ける
40KN / 800 = 50N/mm2
材料をS45Cとした場合 降伏点35Kg/mm2、剪断荷重安全率12から 35 / 12 = 2.9Kg/mm2 以下であれば安全と判断します。 今回の例では、面圧160N/mm2 = 16.3Kg/mm2、 剪断 50N/mm2=5.1Kg/mm2 ゆえ問題ありとなります。
圧縮、剪断応力(ヒンジ部に働く応力)
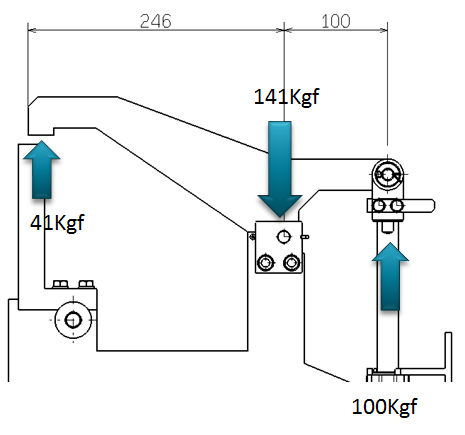
ヒンジ部には軸受が通常使用されます。
滑り軸受けの場合下記の式で面圧を計算します。
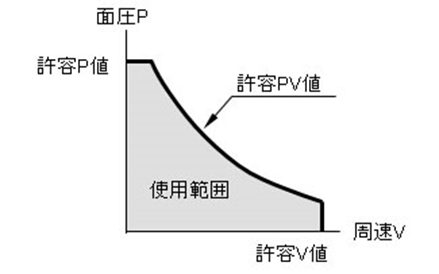
軸受の場合、単純に面圧のみでなく動く速度も考慮に入れるために通常 軸受メーカーのカタログにはPV値が掲載されていますのでこの範囲内で使用する必要があります
![]()
W=141Kgf , d = 12 , L = 12
P= 141 / (12 X 12 ) = 0.98Kgf/mm2
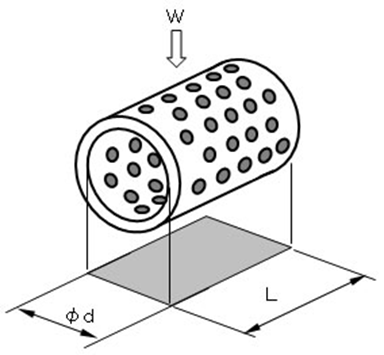
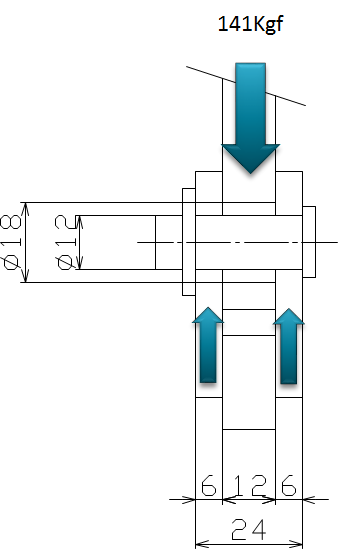
ヒンジ部に使用されるピンには剪断力が右のように働きます。
ピンは2か所で剪断力が働くのでピンの断面積の2倍で応力を受けます。
141 / ( 12 ^2. π / 4) = 1.25Kgf/mm2
面圧、剪断応力ともSS400の安全率を加味した許容応力
7Kg/mm2に対して問題ないと判断できます。
車輪面圧(圧縮)の計算
この例では、車輪をMC NYLON 平面を鋼として計算する。
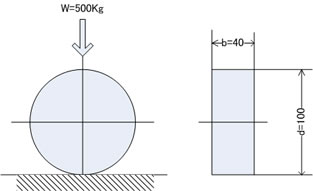
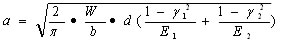
荷重 W = 500 Kgf
車輪幅 b = 40 mm
車輪径 d = 100 mm
車輪圧縮弾性比 E1 = 360 Kg/mm^2
MC NYLON
平面圧縮弾性比 E2 = 21000 Kg/mm^2
鋼
車輪ポアソン比 γ1 = 0.4
MC NYLON
平面ポアソン比 γ2 = 0.3
鋼
接触幅 a = 1.375242248 mm
接触面積 S = 110.0193798 mm^2
圧縮応力 F = 4.544653867 Kgf/mm^2 となる。
内圧を受ける肉厚円筒
内径に比べて肉厚の大きい円筒を肉厚円筒という。
肉厚円筒では内圧によって生じる応力は一様にはならず内壁で最大になり外側に行くほど小さくなる。
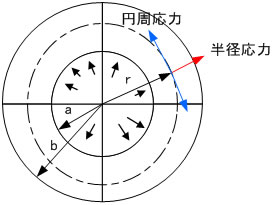 肉厚円筒では右の図に示す円周応力と半径応力を考慮しなければならない。
肉厚円筒では右の図に示す円周応力と半径応力を考慮しなければならない。
a= (内径 ) , b= (外形) , r= (中立半径) p= (圧力), k = b/a, R = r/aとすると各応力は、次の式で表される。
半径応力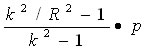
円周応力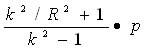
平板の曲げ
円板がその中心に対して対称形の垂直荷重を受け軸対称形のたわみを生じる場合の方程式を示す。
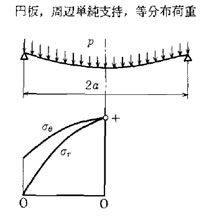
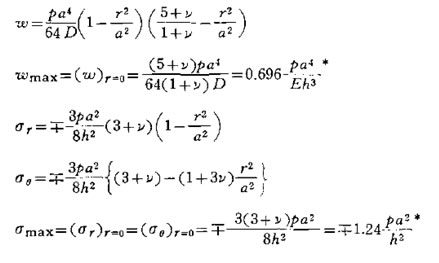
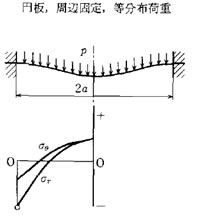
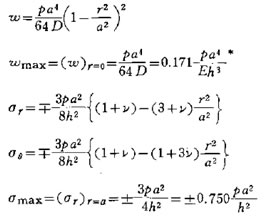
円板等分布最大応力
p= (圧力) , h= (板厚), a= (円板半径)とすると最大応力は、次の式で表される。