ねじり
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
ねじり応力
右の絵のようにスパナでボルトを廻すときに、ボルトには、ねじりモーメントが働いています。 ボルトは ねじられまいとする応力が生じ
ます。 この応力よりも大きいモーメントを与えると ボルトはねじ切れてしまいます。
旋盤で加する物もすぺてねじりモーメントが働きます。 切削材料には曲げ応力、ねじれ応力力、,せん断応力の3種 類の応力が生じます。
丸棒のねじり
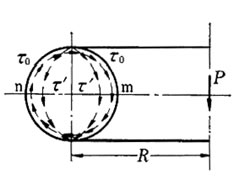
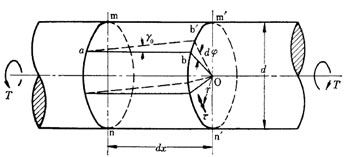
棒に軸線周りの偶力を加えれば、横断面は相対的に回転しようとして、横断面に剪断応力を生じます。 このような現象をねじりと いい、横断面に生ずる剪断応力をねじり応力といいます。
下図において、 丸棒がねじられれば、横断面 m'n' 上の各点は 中心Oの周りに回転する。 この場合、横断面はねじられた後も平面を保ち、各点は中心軸からの距離に比例して回転すると仮定すれば、半径ObはOb'の位置に移動する。
いま mn断面とm'n' 断面との距離を dx とし、両面の相対的回転角をdψとすれば、表面の剪断歪γoは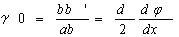 
であるから断面周辺に生ずる剪断応力は
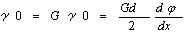展開して
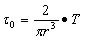となる。
G=せん断弾性係数(鋼の場合8100Kg/mm^2)
例として 丸25mmの軸に32Kg.mのトルクをかける。
2/ (πX12.5^3) X 32 X 1000 = 10.4Kg/mm^2となる。
横断面の相対的回転角dψをねじれ角という。 単位長さあたりのねじれ角をωで表す。 円形および同心円形の断面二次極モーメント Ip は、それぞれπd^4/32、π(d2^4-d1^4)/32であるので 、と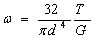
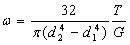なる。
例
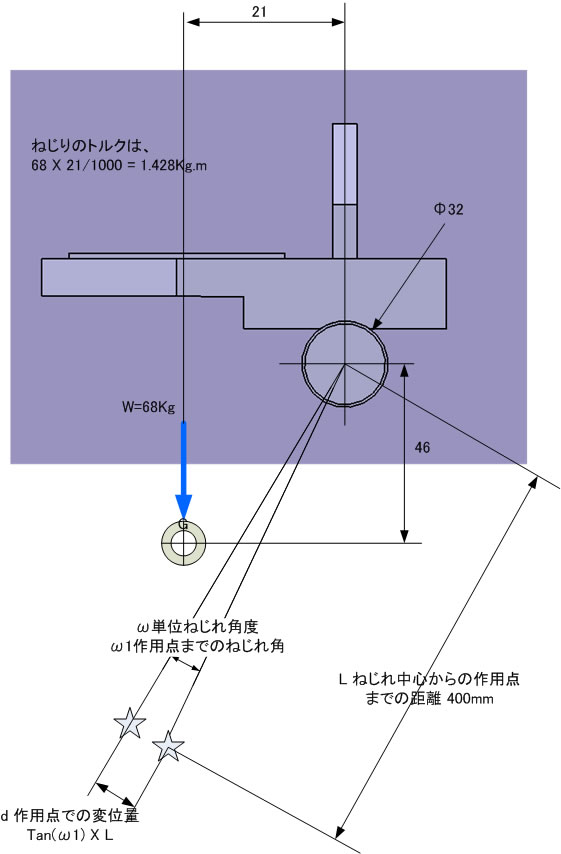
単位はmmで計算するのであればmmに合わせます。
直径 32 mm
、 トルク 1428 Kg.mm
上の条件より68Kg X 21mm = 1428 Kg.mm
せん断弾性係数 8100 Kg.mm2
作用距離 900 mm
L ねじれ中心からの距離 400 mm
ω（単位ねじれ角) 1.71255E-06 rad.mm (1mmあたりの角度)
ω1 作用点でのねじれ角度 0.001541295 rad.mm (単位角度に900をかけたもの）
d 作用点での変位量 0.010760272 mm (TAN(ω1) X 400)
種々の断面のねじり
単位長さのねじれ角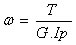
、 捻りの断面係数
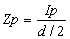、 捻り応力
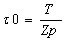で表わされる。
断面形が決まれば Ip = Iy + Iz 、によって容易に Ip を求めることができる。
しかし 上の式が適用できるのは、横断面が円形および同心円形の場合に限られる。
一般にはねじり剛さは T/ω によって定義され、 GIp に等しくない円形以外の断面をもつ棒についてねじり応力およびねじれ角を求めるには弾性学によらねば ならないからここでは主要な断面形について、その結果のみを示す。
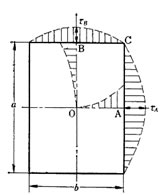
右図、長方形断面棒のねじり応力 長方形断面の棒をねじれば、図のように剪断応力は中心Oからの距離に比例しないで,OA, OB上では図のように分布し、周辺に生ずる剪断応力は辺の中央で最大になる。
それらをτA、τBとし 単位長さのねじれ角をωとすればそれらは で
表される。 正方形の場合は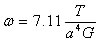
となる。
またA点、B点での最大せん断応力は、それぞれ
、
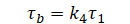で 表される。
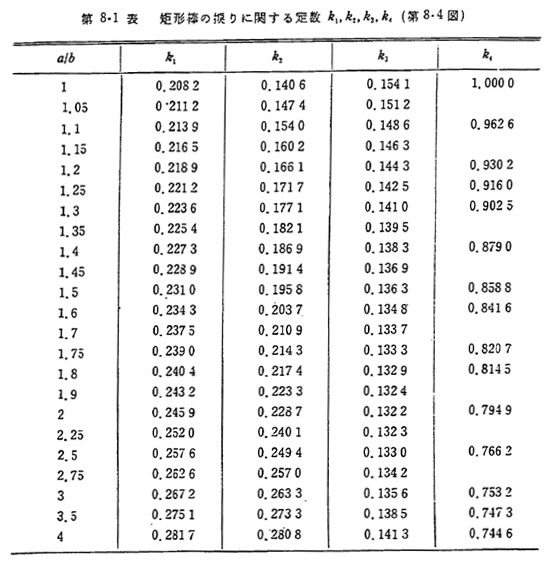
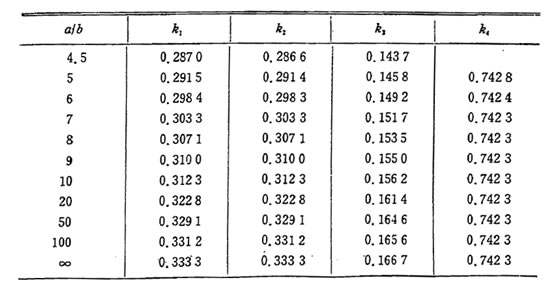
k1,k2,k3は 以下の表より算出する。
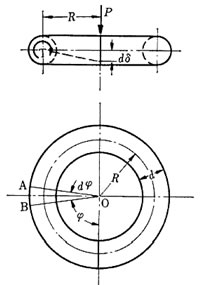
コイルばね
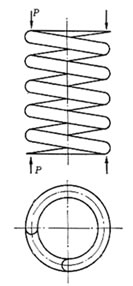棒を円筒形に巻いたものをコイルばねといい、この棒を素線という、素線には円形の横断面のものが多いが長方形断面のものなどもある。
右図のように、コイルぱねに圧縮荷重Pを加えれぱδだけ縮み、通常密着するまではPとδが正比例するように作られている。
コイルぱねは棒が一定の間隔でら旋状に巻かれたものであるが、コイルぱねのピッチ角は小さいから、その応力および歪みを解析する場合には、コイルばねを下左図のような一平面内に巻かれた円輪に置き換え、荷重はその中心に作用すると考える。
そのときのねじりモーメントによる、最大剪断応力は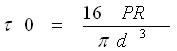
となる。
