応力集中
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
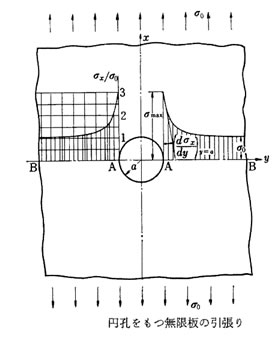 無限に広い板を無限板といい,右図のように円孔をもつ無限板を X軸方向に引張れば、円孔から十分遠く離れた部分には一様な応力σx = σ0 を生ずるが、円孔中心を通って x 軸に直角な断面BBに右のような応力を生ずる。
無限に広い板を無限板といい,右図のように円孔をもつ無限板を X軸方向に引張れば、円孔から十分遠く離れた部分には一様な応力σx = σ0 を生ずるが、円孔中心を通って x 軸に直角な断面BBに右のような応力を生ずる。
そして最大引張応力は円孔縁A点に生じる。 しかし円孔縁を離れるにつれて急速に減少する。.
このような現象を応力集中と いい、このような現象は、円孔がない場合に断面AAが負担していた力が断面ABに一様に分担されないで、主にA点近くに負担されるために生じ、応力はA点に集中するように分布する。
このような応力を集中応力といい、A点における応力分布曲線の勾配を応力勾配という。
結局A点には、円孔がなければ応力σoを生じ、円孔があれば最大引張応力σnmax = 3σo を生じ、その比をαとすれば σ= αmax/ α0 = 3 である。
 αのことを形状係数 あるいは応力集中係数といい、αの基準になる応力σ0を公称応力という。
αのことを形状係数 あるいは応力集中係数といい、αの基準になる応力σ0を公称応力という。
結局αは最大応力が公称応力の何倍であるかを示す係数である。
この場合には円孔のために最大引張応力が3倍に 増大したことになる。
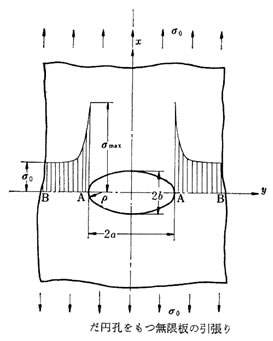
右図のように、だ円孔をもつ無限板を直径方向に引張れば、引張方向に直角な直径の両端Aに最大引張応力(σx)maxを生じる。
a = b ならば だ円は円になり α=3である。 a/b が大きいほどすなわ ち扁平になるほどαは大きくなり、 b = 0 すなわち板にき裂があればき裂の両端 には無限大の応力を生ずることになる。
このことは,荷重が如何に小さくても き裂の両端は塑性変形をすることを意味し、材料がもろければ小さな荷重によっても、両端にき裂を生じ 次第にき裂が拡大 して破壊を招く恐れがある。
このような場合には下図のように、 き裂の両端に円孔をあければ き裂の拡大を防ぐことができる。
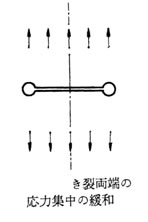
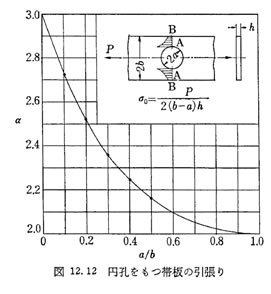
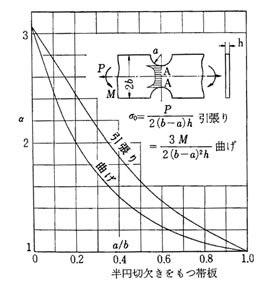
右上グラフに示すように 円孔が大きくなるにつれて、BB断面の断面積が零に近づくと、円孔縁における、応力勾配は小さくなる。 すなわちA点に応力が集中する程度が小さくなるにもかかわらず、形状係数が大きくなる。
そこで、このような場合には、BB断面の平均応力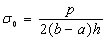 を公称応力とする。 小さな円孔があるとき a/b = 0においてα =3 になり 円孔が大きくなるにつれαは次第に小さくなり a/b = 1 においてα = 2になる。
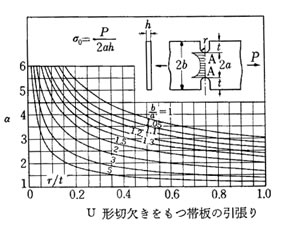
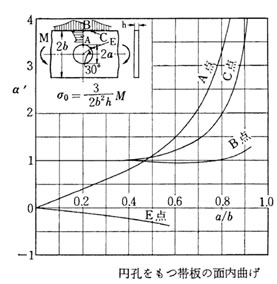
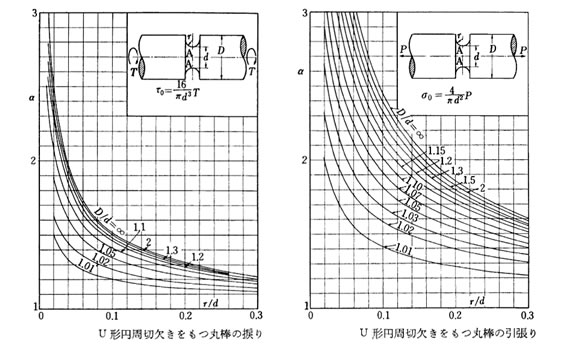
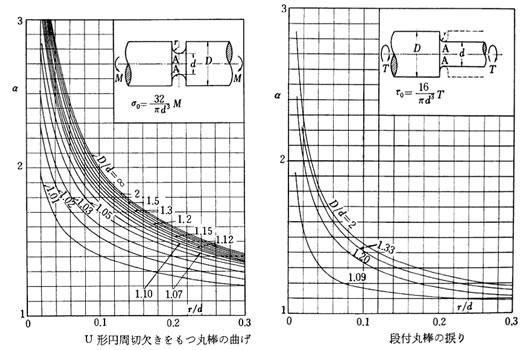
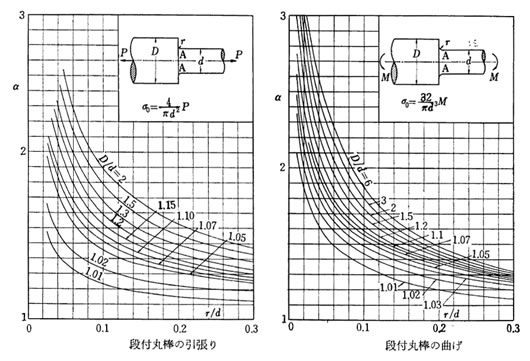
同様に切り欠き形状、その母材に対する切り欠きの比率により応力集中係数は変化する。代表的なグラフを示す。
を公称応力とする。 小さな円孔があるとき a/b = 0においてα =3 になり 円孔が大きくなるにつれαは次第に小さくなり a/b = 1 においてα = 2になる。
同様に切り欠き形状、その母材に対する切り欠きの比率により応力集中係数は変化する。代表的なグラフを示す。