圧縮空気の流れ
日頃より本コンテンツをご利用いただきありがとうございます。
今後、下記サーバに移行していきます。お手数ですがブックマークの変更をお願いいたします。https://kousyou.synology.me
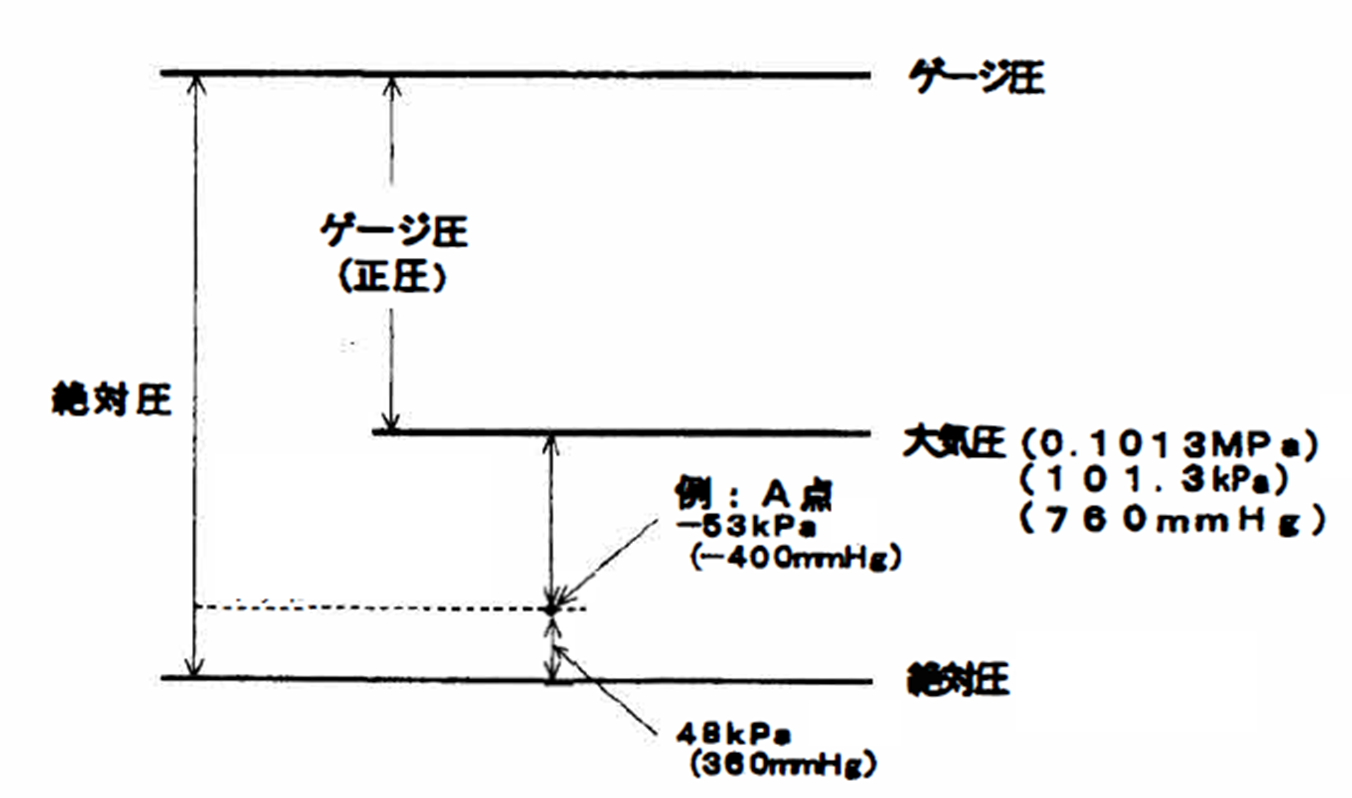
絶対圧力とゲージ圧力
ゲージ圧力と絶対圧力の関係、は次のようになる。
絶対圧力P[MP a abs] ＝ゲージ圧力P[MPaG] ＋大気圧0. 1 MPa
通常工業分野では、ゲージ圧力を使用する。 Gも通常は、つけない。真空機器は、両方使用されているので注意が必要。
エネルギーの式
管内を流れる流体のエネルギーは、管路のどこの部分をとっても等しい。
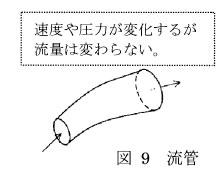これは、流体のもつエネルギーが流速から得られる運動エネルギーと、流体の持つ圧力、および流体の基準位置からの高さで発生する位置エネルギーの和になるためである。
運動エネルギー＋圧力エネルギー＋位置エネルギー = 一定 空気の場合には位置エネルギーはほとんど無視できる。 これをベルヌーイの定理と呼ぶ。
機器を通る流れ
流管中のどこの位置においても、流体の質量流量 は等しくなる。
これを連続の式と呼ぶ。
機器や管内に設けられた狭い断面積のオリフィスを圧縮空気が流れる場合、図に示すよ うに、上流側と下流側の圧力の比が１の時の質量流量が０から圧力比を小さくするにつれて質量流量は増大するが、臨界圧力比 ｂ になると流速は音速に達し、以後圧力比が０まで質量流量は一定になる。
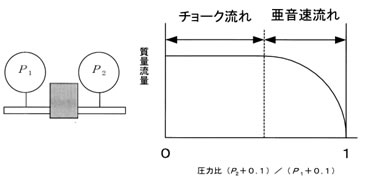この質量流量が飽和する流れをチョーク流れ（閉塞流れ）という。 また、臨界圧力比が b 以上の音速に達しない流れを亜音速流れという。
オリフィスを通過する圧縮空気の質量流量は亜音速流れ、チョーク流れ２つの領域に分けて表される。
臨界圧力比 （P2＋0.1） / （P1＋0.1） = ｂ
音速コンダクタンス 圧縮
空気の流量計算式は国や業界によって様々なものが用いられ、国内では主に有効断面積 S［ｍｍ２］を使用して計算が行われていた。
ＩＳＯでは、１９８９年に音速コンダクタンスＣ［ｄｍ３／（ｓ・ｂａｒ）］と臨界圧力比ｂを用いることになる。
空気圧機器の内部流路構造は複雑なので、流れのチョークする時の機器前後の圧力比は機器によってまちまちとなる。そこで、差圧式流量特性試験により臨界圧力比ｂと音速コンダクタンスＣを求め、ｂをパラメータとする楕円関数の式で流量を表す。
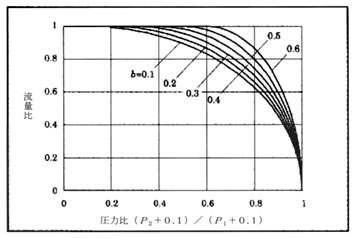図１１流量特性線図
音速コンダクタンスＣと有効断面積Ｓの関係は、臨界圧力比ｂが0.5の場合に下記の換算であらわすことができる。 S［ｍｍ2］ = 5.0 X C
また、現在でも大型の機器（呼び口径20mm以上）では有効断面積が用いられている。
流量計算式
チョーク流れ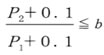
のとき
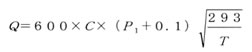
亜音速流れ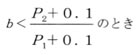
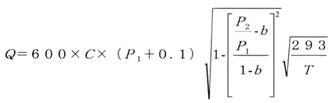
Q : 圧縮空気の流量［ｄｍ3/ｍｉｎ（ＡＮＲ）］
Ｃ : 音速コンダクタンス［ｄｍ3/（ｓ・ｂａｒ）］
P1 : 上流側圧力［MPａ］
P2 : 下流側圧力［MPａ］
T : 空気温度［K］ *注 dm3 = L(リットル) 参考
有効断面積の流量計算式
チョ一ク流れ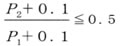 
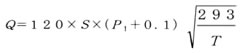
亜音速流れ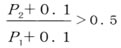 
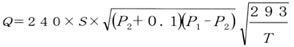
有効断面積［ｍｍ２］
空気が穴（オリフィス）を通った後に空気の流れは、オリフィスの径よりも小さくなる。 これを有効断面積という。
従来ＪＩＳで流量特性の代表値として規定された有効断面積は、バルブ等の実流量に基づく、抵抗を等価のオリフィス断面積に換算したもので、［mm2］の単位で表される。
測定は下記のような放出法で行われる場合が多い。
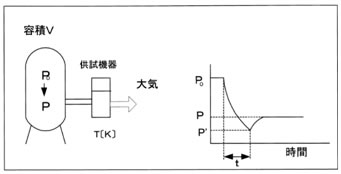圧力‐Ｐ0［MPａ］に圧縮空気が充填された内容積 V［L] の容器に供試機器を直結し、容器内圧力が、P'［MPａ］になるまで供試機器をt［sec］間開けて空気を大気放出し、一定に落ち着いた後の残存圧力P［MPａ］を測定して次式から有効断面積 S［mm2］を算出する。 ただし室温を Ｔ［K］とする。
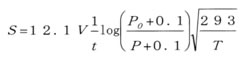
ＪＩＳは、 Ｐ0 = 0.6MPａを下回らない値、 P = 0.25MPａ、t = 約 5 secになるような Vの選定を規定している。 （チョーク流れ、断熱変化の範囲）
例１
音速コンダクタンス4dm3/（s・ｂａｒ）、臨界圧力比 0.3 のバルブの上流側圧力が0.6MPａ、下流側圧力が0.4MPａ、温度２０℃のときの空気流量は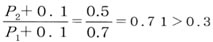
なので亜音速流れの式より
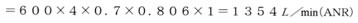
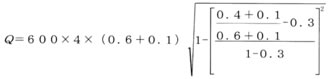
シリンダー空気消費量
φ100-ST500のシリンダーが5kg/Cm^2 圧力で3秒で動作する場合
エアーの消費量はN(標準状態).L（リットル）.min（分）で表す。
シリンダーの体積10^2.π/4 x 50 / 1000 =3.9L 3.9 X (5 +1) = 23.4NL
1分間連続で動作させた場合のエアー消費量を計算する。
60/3 X 23.4 = 468NL/minとなります。